МАТЕМАТИКА 6.РАЗРЕД

 

Недеља, 7.јун 2020.

ОБАВЕШТЕЊЕ:

 

Због седнице која је заказана за уторак у 9 сати, обавештавам ученике који желе да одговарају у циљу поправљања оцене, да време испитивања померам за 8 сати. Све остало остаје исто.

 Четвртак, 4.јун 2020.

 

 

 

 

 

 

 

 

 

петак, 29. мај

 

Драги шестаци, јуче и данас  је била усмена провера, а и данас је последњи час на ТВ учионици. Разговарао сам са већином вас, али ипак са некима нисам успео да успоставим контакт иако сам на време сваког од вас обавестио о данашњој провери.

Према одлуци Министарства, настава на даљину траје још две недеље, и то време ћемо искористити за обнављање и утврђивање градива које смо прешли у овом разреду.

 НАСТАВИТЕ ДА ПРАТИТЕ ОВАЈ БЛОГ, ЈЕР ВАС ОЧЕКУЈУ ВАЖНА ОБАВЕШТЕЊА. Такође ћу вам постављати и лекције које треба да обновите.

За почетак, обновите за викенд лекцију"однос страница и углова у троуглу" која се налази на страни 46-50 у Уџбенику.

Домаћи задатак: написати правила из те лекције (плави текст, са сликом слона у углу)

Среда 27.мај
час 140.

 Обавештење:

Осмаци и седмаци су завршили са провером знања, ви сте на реду сутра, у четвртак, 28. маја. У времену од 10 сати (ујутро) до 13 сати очекујте мој позив преко Вибера. Зваћу вас на бројеве које сте ми доставили. 

Данашњи задатак је да погледате ТВ час на коме је обнављање лекције о површини четвороугла и троугла.

Такође обновите све области које смо радили у периоду наставе на даљину: четвороуглови, углови четвороугла, вектори, конструкције четвороуглова, површине троугла и четвороугла.

уторак, 26.мај
час 139.

ОБАВЕШТЕЊЕ:

провера ће бити крајем ове недеље.

понедељак, 25. мај
час 138.

четвртак 21.мај 2020.
час 135.

Среда, 20.мај 2020.
 час 134.

ОБАВЕШТЕЊЕ ЈЕ ИСПОД ЛЕКЦИЈЕ!!!!

 Понедељак, 18. мај 2020.
час 133.

На ТВ учионици је кренуло понављање лекција које смо учили. Данас је причано о површини паралелограма. Пратите ТВ учионицу и наставу на блогу!!

ЧЕТВРТАК, 14.мај 2020.
час 132.

ПОВРШИНА ТРОУГЛА,

утврђивање

Домаћи задатак: 

Среда 13.мај 2020.
час 131.

Уторак, 12.мај 2020.
час 130.

Понедељак, 11.мај 2020
час 129.

Драги шестаци, данас сте радили писмену проверу. Задаци ће бити прегледани у току недеље, после чега ћете мејлом добити коментар и обавештење о оцени која ће бити унета у дневник. 

петак, 8.мај 2020.

четвртак, 7.мај 2020.
час 126.

Среда 6.мај 2020.
час 125.

Уторак 5. мај 2020.
час 124.


Данашњи час има исту тему и наслов као и јуче:

ДОПУЊАВАЊЕ И РАЗЛАГАЊЕ ГЕОМЕТРИЈСКИХ ФИГУРА

Настављамо са вежбањем. Ваши се задаци налазе на 185. страни Уџбеника: 6. и 7. задатак.

Понедељак, 4.мај 2020.
час 123.

среда, 29.април 2020.
час 122.

ПОВРШИНА ПРАВОУГАОНИКА И КВАДРАТА

утврђивање

понављамо: 

Површина је геометријски појам који означава меру величине геометријске слике у равни.

Тачка и линија немају површину, односно њихова површина је нула.

 Раван има бесконачну површину.

Мерне јединице

Према СИ систему јединица мера, који је и код нас на снази, основна мерна јединица површине је квадратни метар (m²), а могу се користити и из ње изведене величине:

• 1 dm² = 0.01 m²
• 1 cm² = 0.0001 m²
• 1 mm² = 0.000001 m²

• 1 ar = 100 m²
• 1 ha = 10 000 m²
• 1 km² = 1 000 000 m² 

Површина правоугаоника и квадрата серачуна као производ две суседне странице!!

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                      

Домаћи задатак на слици испод

уторак, 28.април 2020.
час 121.

ПОЈАМ ПОВРШИНЕ. ПОВРШИНА ПРАВОУГАОНИКА И КВАДРАТА.

Појам површине свако од нас интуитивно прихвата; проблем настаје када треба дефинисати тај појам. једна од бољих дефиниција које су примерене вашем узрасту је

Површина је геометријски појам који означава меру величине геометријске слике у равни. Тачка и линија немају површину, односно њихова површина је нула. Раван има бесконачну површину. 

Површина је такође и део тела у простору који је изложен спољашњости. Мерењем површина су се бавили још стари Египћани, али су га до нивоа науке подигли тек  стари Грци. Код њих се површина неке геометријске слике израчунавала тако што се низом трансформација та слика претвара у квадрат исте површине. Потом се измере странице квадрата и лако израчуна површина. Од тих дана је израчунавање површине добило други назив: квадратура. 

 У  СИ систему јединица (то је систем који се примењује код нас и у највећем делу света), стандардна јединица површине је  метар квадратни, или квадратни метар (пише се као m²), што је површина квадрата чије су странице дуге по један метар. Облик са површином од три квадратна метра би имао исту површину као и три таква квадрата.

Мерне јединице

Према СИ систему јединица мера, који је и код нас на снази, основна мерна јединица површине је квадратни метар (m²), а могу се користити и из ње изведене величине:

• 1 dm² = 0.01 m²  (ретко се користи)
• 1 cm² = 0.0001 m²(ретко се користи)
• 1 mm² = 0.000001 m² = 10^-6m² (користи се за мерење површине пресека жице у електротехници и сл)

За мерење површине терена користе се веће мере:

• 1 ar = 100 m² = 10²m²  (један ар)
• 1 ha = 10 000 m² = 10⁴m² (један хектар)
• 1 km² = 1 000 000 m² = 10⁶m² (један квадратни километар)

Појам површине лако можемо да схватимо ако нашу раван поделимо на "коцкице" тј. паралелним водоравним и вертикалним линијама, које су увек на подједнаком растојању јњдна од друге. На тај начин добијамо подједнаке квадратиће. Ако изаберемо један квадратић као нашу мерну јединицу, онда једноставним пребројавањем квадратића добијамо меру површине слике:

Ако је наша мерна јединица један квадратић, онда, на слици изнад, и једна и друга уоквирена фигура имају величину 12 квадратића.

Геометријске фигуре као што су квадрат и правоугаоник је најлакше поделити на квадратиће због њиховог облика:

Њихова се површина рачуна као производ две суседне странице!!

  Домаћи задатак: уџбеник, страна 183, задаци 2 и 3




















понедељак, 27.април 2020.
час 120

 

 

 

ДЕЛТОИД 

 

 

Делтоид је четвороугао са следећим особинама:

1. има два пара ПОДУДАРНИХ СУСЕДНИХ страница

2. дијагонале му се СЕКУ ПОД ПРАВИМ УГЛОМ

3. УГЛОВИ које заклапају РАЗЛИЧИТЕ СТРАНИЦЕ су ПОДУДАРНИ

4. У делтоид се МОЖЕ УПИСАТИ кружница. Центар уписане кружнице је пресек симетрала једнаких углова.

ДОМАЋИ ЗАДАТАК: одговорити на питања:
1. Шта је четвороугао?
2. Колики је збир спољашњих а колики унутрашњих углова сваког четвороугла?
3. како се деле четвороуглови?
4. Дефиниши : паралелограм, ромбв, правоугаоник, квадрат, трапез и делтоид.

Четвртак 23.април 2020.

час 119.

 

Добио сам неколико мејлова са домаћим задацима, али нико није послао мејл у коме треба да потврдите да сте прочитали и разумели обавештење о писменом задатку. Зато га постављам поново:

 У понедељак 11. маја, радићете писмени задатак. Тога дана ће свако од вас у 12 сати добити задатке које треба да уради, фотографише и те фотографије пошаље на мој мејл најкасније до 13 сати и петнаест минута. Задатке ћете добити на мејл адресе са којих сте ми се до сада јављали. Задаци ће бити из области које смо радили у периоду од другог писменог: Троугао, правоугли координатни систем, Пропорционалност и пропорције и четвороугао. Свако од вас ће имати задатке исте тежине али са другачијим подацима.

Напомињем да задатке који пристигну после задатог рока нећу узимати у обзир. Молим да овај писмени задатак схватите најозбиљније, јер ћу вам на основу њега дати једну од оцена. АКО ВАМ ЈЕ БИЛО ШТА НЕЈАСНО у вези овог обавештења ПИТАЈТЕ НА ВРЕМЕ!! ТАКОЂЕ, ДА МИ СЕ СВИ ЈАВИТЕ ДО ПЕТКА, ДА СТЕ ПРОЧИТАЛИ И РАЗУМЕЛИ ОБАВЕШТЕЊЕ!!

 

 

ЧЕТВОРОУГАО

систематизација, први део

 

 

Поновићемо у најкраћим цртама оно што смо научили о четвороуглу:

 

 Четвороугао је геометријска фигура коју чини део равни ограничен са четири странице. Има четири темена и четири угла.  

 

Збир унутрашњих углова сваког четвороугла је 360⁰ 

α +β + γ + δ = 360⁰

Збир спољашњих углова сваког четвороугла је 360⁰

α₁ +β₁ +γ₁ +δ₁ = 360⁰

Сваки четвороугао има тачно две дијагонале. Дијагонала је дуж која спаја два несуседна темена.

 

 

 

 

 Четвороуглови се деле на конвексне и неконвексне.

 Четвороугао је конвексан ако дуж која спаја било које две тачке унутрашње области остаје унутар четвороугла.

 Четвороугао је неконвексан ако дуж која спаја било које две тачке унутрашње области излази из  ње.

 

 

Четвороуглови се деле на:

1) Паралелограми (имају по два пара паралелних страница) 
2) Трапези (имају један пар паралелних страница) 

3) Трапезоиди (немају паралелне странице)

У ПАРАЛЕЛОГРАМЕ СПАДАЈУ



ПАРАЛЕЛОГРАМ:

Паралелне странице су му једнаке Наспрамни углови су му  једнаки а  суседни  су суплементни

Дијагонале се међусобно полове Централносиметрична је фигура 

 


КВАДРАТ:
Сва четири угла су му права
Све странице су му једнаке
Дијагонале су му једнаке и међусобно се полове под правим углом
Централно симетрична је фигура: у њега се може уписати кружница, око њега се може описати кружница.
Има  4 осе симетрије






ПРАВОУГАОНИК:

Сва четири угла су му права
Паралелне странице су му једнаке
Дијагонале су му једнаке и међусобно се полове
Централносиметрична фигура: у њега се не може уписати кружница, око њега се може уписати кружница
Има 2 осе симетрије

РОМБ:

Све четири станице су му једнаке

Наспрамни углови су му једнаки а суседни су суплементни

Дијагонале му се међусобно полове под правим углом, зато се у њега може уписати кружница. Централносиметрична фигура, има две осе симетрије

 

ДОМАЋИ ЗАДАТАК: конструисати ромб коме је једна страница 8 цм и један угао 60 степени.

среда 22.април 2020
час 118

 ВАЖНО!!ВАЖНО!!ВАЖНО!!

ВАЖНО!!ВАЖНО!!

Драги шестаци, у понедељак 11. маја, радићете писмени задатак. Тога дана ће свако од вас у 12 сати добити задатке које треба да уради, фотографише и фотографије пошаље на мој мејл најкасније до 13 сати и петнаест минута. Задатке ћете добити на мејл адресе са којих сте ми се до сада јављали. Задаци ће бити из области које смо радили у периоду од другог писменог: Троугао, правоугли координатни систем, Пропорционалност и пропорције и четвороугао. Свако од вас ће имати задатке исте тежине али са другачијим подацима.

Напомињем да задатке који пристигну после задатог рока нећу узимати у обзир. Молим да овај писмени задатак схватите најозбиљније, јер ћу вам на основу њега дати једну од оцена. АКО ВАМ ЈЕ БИЛО ШТА НЕЈАСНО у вези овог обавештења ПИТАЈТЕ НА ВРЕМЕ!! ТАКОЂЕ, ДА МИ СЕ СВИ ЈАВИТЕ ДО ПЕТКА, ДА СТЕ ПРОЧИТАЛИ И РАЗУМЕЛИ ОБАВЕШТЕЊЕ!!

 

Данашња наставна јединица је 

ДЕЛТОИД 

 

  

 

Делтоид је четвороугао са следећим особинама:

1. има два пара ПОДУДАРНИХ СУСЕДНИХ страница

2. дијагонале му се СЕКУ ПОД ПРАВИМ УГЛОМ

3. УГЛОВИ које заклапају РАЗЛИЧИТЕ СТРАНИЦЕ су ПОДУДАРНИ

4. У делтоид се МОЖЕ УПИСАТИ кружница. Центар уписане кружнице је пресек симетрала једнаких углова.

 ДОМАЋИ ЗАДАТАК:

Нацртати делтоид и правилно обележити његове елементе. НАПИСАТИ које су особине делтоида.

понедељак,21.април 2020
час 117.

ВИСИНА ТРАПЕЗА

Висина трапеза је вертикално растојање између основица трапеза.

 

Са доњом основицом гради прав угао.

Задатак 1:  конструисати једнакокраки трапез ABCD чије су основице АВ = 5цм,  СD = 3цм а висина h = 2cm.

 

ДОМАЋИ ЗАДАТАК: ово је анализа, а ви ћете урадити У ВАШИМ СВЕСКАМА исту ову анализу, а затим и КОНСТРУКЦИЈУ.

среда, 15.април 2020.

час 116

 

КОНСТРУКЦИЈА ТРАПЕЗА

утврђивање

 

Обавезно погледајте лекцију на линку:

https://mojaskola.rtsplaneta.rs/show/1358117/529/os6-matematika-konstrukcija-trapeza-utvrdjivanje

Као и код троугла и паралелограма, и конструкција трапеза захтева АНАЛИЗУ и КОНСТРУКЦИЈУ.

ВАШ ЗАДАТАК ЈЕ ДА ПАЖЉИВО И СА РАЗУМЕВАЊЕМ ОДРАДИТЕ У СВЕСЦИ ПРИМЕР 2 НА СТРАНИ 176 УЏБЕНИКА.

уторак, 14.април 2020.

час 115

 

 

Драги шестаци, после првих двадесетак дана добили сте и прве оцене активности. Већина вас је била и остала  врло активна, и сходно томе и добро оцењена. Разумљиво је да нисмо могли сви одмах и у истој мери да се пребацимо на овакав начин наставе, из много разлога који су мање или више оправдани. Ускоро ће бити почето и са бројчаним оцењивањем пошто смо неке области завршили. Ваше је да пратите ТВ учионицу, и наставу коју држим преко овог блога, и да се потрудите најбоље што можете у овом тренутку. По задацима које добијам видим да напредујете, и то је за сваку похвалу. Ипак, још увек нисам са свима успоставио контакт, јер очигледно да неки родитељи и ученици не схватају у довољној мери озбиљност ситуације у којој се налазимо и начина на који покушавамо да превазиђемо ту ситуацију.

 

 

Данашња наставна јединица је 

КОНСТРУКЦИЈА ТРАПЕЗА

Обавезно погледајте лекцију на линку:

 https://mojaskola.rtsplaneta.rs/show/1356265/529/os6-matematika-konstrukcija-trapeza-obrada

 Као и код троугла и паралелограма, и конструкција трапеза захтева АНАЛИЗУ и КОНСТРУКЦИЈУ.

ВАШ ЗАДАТАК ЈЕ ДА ПАЖЉИВО И СА РАЗУМЕВАЊЕМ ОДРАДИТЕ У СВЕСЦИ ПРИМЕР 1 НА СТРАНИ 175 УЏБЕНИКА.

Понедељак, 13.април,2020.
час 113-114

данашња тема је 

ТРАПЕЗ. СВОЈСТВА ТРАПЕЗА, СРЕДЊА ЛИНИЈА ТРАПЕЗА И ТРОУГЛА.

Овај час треба ОБАВЕЗНО да одгледате на следећој адреси:

https://mojaskola.rtsplaneta.rs/show/1353178/529/os6-matematika-srednja-linija-trougla-i-trapeza

ПРВО ДА ПОНОВИМО:

ТРАПЕЗ ЈЕ ЧЕТВОРОУГАО СА ЈЕДНИМ ПАРОМ ПАРАЛЕЛНИХ СТРАНИЦА

Његови елементи су:

• ДВЕ ПАРАЛЕЛНЕ ОСНОВИЦЕ, различитих дужина
• КРАЦИ ТРАПЕЗА су странице c и d, и оне могу бити исте дужине или различите
• ВИСИНА  трапеза h је вертикално растојање између основица
• СРЕДЊА ЛИНИЈА ТРАПЕЗА m је линија која СПАЈА СРЕДИНЕ КРАКОВА и она је ПАРАЛЕЛНА СА ОСНОВИЦАМА
• Унутрашњи и спољашњи УГЛОВИ ТРАПЕЗА
• ДИЈАГОНАЛЕ ТРАПЕЗА 

Разликујемо три врсте трапеза:

1. општи облик, такозвани "обичан трапез", слика 1
2. Једнакокраки трапез, слика2
3. Правоугли трапез, слика 3

обичан трапез

једнакостраничан трапез

правоугли трапез

Једнакостраничан трапез је осносиметрична фигура, за разлику од обичног и правоуглог трапеза. Има два пара подударних углова и две једнаке дијагонале.Углови на истој основици су му подударни!!

Правоугли трапез има два права угла.

УГЛОВИ НА КРАЦИМА ТРАПЕЗА СУ СУПЛЕМЕНТНИ!!!

СРЕДЊА ЛИНИЈА ТРАПЕЗА m је линија која СПАЈА СРЕДИНЕ КРАКОВА и она је ПАРАЛЕЛНА СА ОСНОВИЦАМА (слика испод)

средња линија трапеза m

СРЕДЊА ЛИНИЈА ТРАПЕЗА ЈЕ ЈЕДНАКА ПОЛОВИНИ ЗБИРА ОСНОВИЦА,  израчунава се по формули:

m = (a + b): 2

Домаћи задатак: УЏБЕНИК, страна 174, задатак 7 и 8.













четвртак, 9.април 2020
час 112



Данашња наставна јединица је 

ТРАПЕЗ

Ова наставна јединица је одржана као други час на ТВ учионици, и ево вам линк да се подсетите:

https://mojaskola.rtsplaneta.rs/show/1347157/529/os6-matematika-trapez-svojstva-trapeza

Трапез припада четвороугловима. ТРАПЕЗ ЈЕ ЧЕТВОРОУГАО СА ЈЕДНИМ ПАРОМ ПАРАЛЕЛНИХ СТРАНИЦА. Приказан је на слици доле:


 


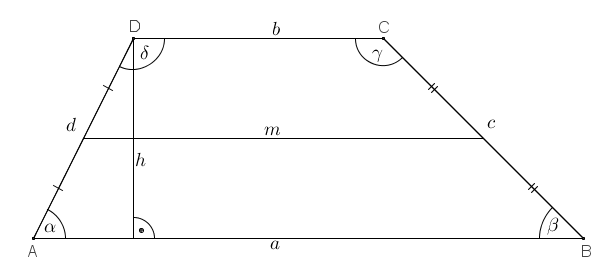
Његови елементи су (на слици горе):

• ДВЕ ПАРАЛЕЛНЕ ОСНОВИЦЕ, а и b, које су РАЗЛИЧИТИХ ДУЖИНА
• КРАЦИ ТРАПЕЗА су странице c и d, и оне могу бити исте дужине или различите, као на слици изнад
• ВИСИНА  трапеза h је вертикално растојање између основица
• СРЕДЊА ЛИНИЈА ТРАПЕЗА m је линија која СПАЈА СРЕДИНЕ КРАКОВА и она је ПАРАЛЕЛНА СА ОСНОВИЦАМА
• Унутрашњи и спољашњи УГЛОВИ ТРАПЕЗА ( спољашњи углови су приказани на слици испод)
• ДИЈАГОНАЛЕ ТРАПЕЗА приказане на слици испод и обележене са d₁ и d₂

Ваш ДОМАЋИ ЗАДАТАК је да погледате емисију на линку који сам дао, да у свесци нацртате трапез и прикажете његове елементе.














Среда, 8.април 2020.
час 111

САБИРАЊЕ И ОДУЗИМАЊЕ ВЕКТОРА

систематизација


Драги петаци, потпуно ми је јасно да вам је лекција о векторима тешка: али то је предвиђено планом и програмом, а и учили смо их још у петом разреду.

Схватите векторе на следећи начин: ВЕКТОРИ СУ ОРИЈЕНТИСАНЕ ДУЖИ. Шта то значи? Јесу дужи, али не обичне дужи, које смо дефинисали ксо део праве ограничен са две тачке. Те дужи на једном крају имају стрелицу. 
Та стрелица показује СМЕР вектора.
Дужина дужи показује ИНТЕНЗИТЕТ вектора.
 Права којој та дуж припада назива се ПРАВАЦ вектора.
Сваки правац има два смера: као нпр. ваш аутобус саобраћа на правцу Стамница-Петровац, али у два смера: од села до града и од града до села.

Ако имамо две оријентисане дужи, дакле два вектора, који имају исту дужину (интензитет) исти правац (припадају истој правој или паралелним правама) а супротан смер (супротне стрелице) онда се они називају СУПРОТНИ ВЕКТОРИ.

СУПРОТНИ ВЕКТОРИ СУ БИТНИ КОД ОДУЗИМАЊА ВЕКТОРА!


!!!!!!!!! ВАЖНО!!!!!!! 

И КОД САБИРАЊА И КОД ОДУЗИМАЊА ПОСТОЈЕ ДВЕ ГРАФИЧКЕ МЕТОДЕ: МЕТОДА ПАРАЛЕЛОГРАМА И МЕТОДА ТРОУГЛА. ПОКАЗУЈЕМ ВАМ МЕТОДУ ПАРАЛЕЛОГРАМА ЈЕР ЈЕ ВЕЗАНА ЗА ТЕМУ КОЈУ СМО УПРАВО УЧИЛИ, А ТО ЈЕ ПАРАЛЕЛОГРАМ!!!

И САБИРАЊЕ И ОДУЗИМАЊЕ СЕ РАДИ НА ИСТИ НАЧИН. ГЛЕДАТЕ ПРВО САБИРАЊЕ

 НАЈВАЖНИЈЕ ЈЕ ДОВЕСТИ ВЕКТОРЕ У ПОЛОЖАЈ КАО НА СЛИЦИ ИСПОД, а то се постиже ТРАНСЛАЦИЈОМ :

слика 1

 ТРАНСЛАЦИЈА ЈЕ ПОМЕРАЊЕ ВЕКТОРА ДУЖ ПАРАЛЕЛНИХ ПРАВИХ, КАКО БИСМО ИХ ДОВЕЛИ У ИСТИ ПОЧЕТАК (слика испод)

Зелени вектор померамо паралелно ПОМОЋУ ДВА ТРОУГЛА док његов почетак не поклопимо са почетком црвеног вектора. Када то урадимо добијамо положај као на слици 1.

ЗАТИМ КОНСТРУИШЕМО ПАРАЛЕЛОГРАМ!!! (погледајте како смо то радили) ДУЖА ДИЈАГОНАЛА ДОБИЈЕНОГ ПАРАЛЕЛОГРАМА ЈЕ ЗБИР ДВА ВЕКТОРА. ПОЧЕТАК ТОГ ЗБИРНОГ ВЕКТОРА ЈЕ У ТАЧКИ ИЗ КОЈЕ ПОЛАЗЕ ДВА ВЕКТОРА КОЈА САБИРАМО!!!!!!!!!!!!!!!! (слика 3)

ОДУЗИМАЊЕ ВЕКТОРА:

Ако имамо два вектора  а и b ВАЖНО ЈЕ КОЈИ ОД КОГА ОДУЗИМАМО. Ако је   b - а, ОНДА ВЕКТОР а ПРВО ПРЕУСМЕРИМО У СУПРОТНИ СМЕР (једноставно окренемо стрелицу на други крај) а онда ТРАНСЛАЦИЈОМ ДОЂЕМО ОПЕТ ДО СЛИКЕ1!!!

КОНСТРУИШЕМО ПАРАЛЕЛОГРАМ. РЕЗУЛТАТ ЈЕ КРАЋА ДИЈАГОНАЛА. ПОЧЕТАК ВЕКТОРА ЈЕ  НА СТРЕЛИЦИ УМАЊИОЦА (а ).

 

Уторак, 7.април 2020.
час 110

САБИРАЊЕ И ОДУЗИМАЊЕ ВЕКТОРА

утврђивање

ПОНОВИМО НАЈОСНОВНИЈЕ О ВЕКТОРИМА:

•  ВЕКТОРИ СУ ОРЈЕНТИСАНЕ ДУЖИ, КОЈЕ ИМАЈУ СВОЈ ПРАВАЦ, СМЕР И ИНТЕНЗИТЕТ
• НАЈЧЕШЋЕ ИХ КОРИСТИМО У ФИЗИЦИ ЗА ОПИС ПОЈЕДИНИХ ВЕЛИЧИНА (КРЕТАЊЕ, СИЛА ...)
• СМЕР ПРЕДСТАВЉАМО СТРЕЛИЦОМ, ПРАВАЦ ЈЕ ПРАВА КОЈОЈ ПРИПАДА ДУЖ, А ИНТЕНЗИТЕТ ЈЕ ДУЖИНА ДУЖИ.
• ВЕКТОРИ КОЈИ ИМАЈУ ИСТИ ПРАВАЦ И ИНТЕНЗИТЕТ А СУПРОТАН СМЕР НАЗИВАЈУ СЕ СУПРОТНИ ВЕКТОРИ.
• ВЕКТОРЕ САБИРАМО НАДОВЕЗИВАЊЕМ
• ВЕКТОРЕ ОДУЗИМАМО ТАКОЂЕ НАДОВЕЗИВАЊЕМ, АЛИ ПРВО МОРАМО ВЕКТОР КОЈИ ОДУЗИМАМО ДА ПРЕОРЈЕНТИШЕМО (ОКРЕНЕМО СТРЕЛИЦУ9 У ЊЕМУ СУПРОТАН ВЕКТОР.

На слици испод је приказано сабирање два вектора.

Домаћи: саберите ова иста два вектора, на исти начин, у свескама за домаћи.













Понедељак, 6.април, 2020.
час 109. 



                                 ОДУЗИМАЊЕ ВЕКТОРА


 

Драги шестаци, овај блог има ограничење уноса, тако да сам морао да обришем старије лекције да бих направио место за нове. Сачувао сам старе лекције, па, ако неком од вас буду потребне, могу да вам их пошаљем електронском поштом.

Kада одузимамо векторе, у ствари сабирамо негативне векторе. Негативан вектор има исти правац и интензитет, а супротан смер од оригиналног вектора

Да би одузели два вектора, користићемо методу за сабирање – методу  надовезивања, само што треба један од вектора да окренемо у њему супротни. То се практично ради тако што само преместимо стрелицу (у доњем случају плавог вектора) са једног на други крај. Правац и интензитет не мењамо!!!






Пример 1: Методом надовезивања одузети векторе:

Решавамо као што смо рекли. Видите на слици да је плави вектор задржао интензитет (тј. дужину дужи) правац (паралелан је са горњим плавим вектором) само је променио смер (стрелица премештена на други крај)

Домаћи задатак: саберите и одузмите векторе са слике 1 и са слике 2 (слика доле)

линк за векторе

https://www.youtube.com/watch?v=kxOc2VDlU3Q