МАТЕМАТИКА 5.РАЗРЕД

 

  Недеља, 7.јун 2020.

ОБАВЕШТЕЊЕ:

 

Због седнице која је заказана за уторак у 9 сати, обавештавам ученике који желе да одговарају у циљу поправљања оцене, да време испитивања померам за 8 сати. Све остало остаје исто.

 Четвртак, 4.јун 2020.

 

 

 

 

 

 

 

 

 

 

 

петак, 29. април

 

Драги петаци, данас је била усмена провера, а и данас је последњи час на ТВ учионици. Разговарао сам са већином вас, али ипак са некима нисам успео да успоставим контакт иако сам на време сваког од вас обавестио о данашњој провери.

Према одлуци Министарства, настава на даљину траје још две недеље, и то време ћемо искористити за обнављање и утврђивање градива које смо прешли у овом разреду.

 НАСТАВИТЕ ДА ПРАТИТЕ ОВАЈ БЛОГ, ЈЕР ВАС ОЧЕКУЈУ ВАЖНА ОБАВЕШТЕЊА. Такође ћу вам постављати и лекције које треба да обновите.

За почетак, обновите за викенд лекцију "ЦЕНТРАЛНА СИМЕТРИЈА", страна 82 у Уџбенику. 

Домаћи задатак: произвољни петоугао пресликати прво централном а затим и осном симетријом.

 

 

 

 

Среда, 27. мај

час 140.

ОБАВЕШТЕЊЕ:

 

данас је завршена провера знања у седмом разреду. Сутра ће бити у шестом, тако да сте ви на реду у петак, 29.маја. Свакога од вас ћу позвати преко Вибера: ако ми неко није послао број на који да зовем, нека то што пре учини!

Позив очекујте у времену од 10 до 13 часова наведеног дана.

 Тема данашњег часа је наставак јучерашњег часа, тј.

ПРИМЕНА СИМЕТРАЛЕ ДУЖИ И УГЛА

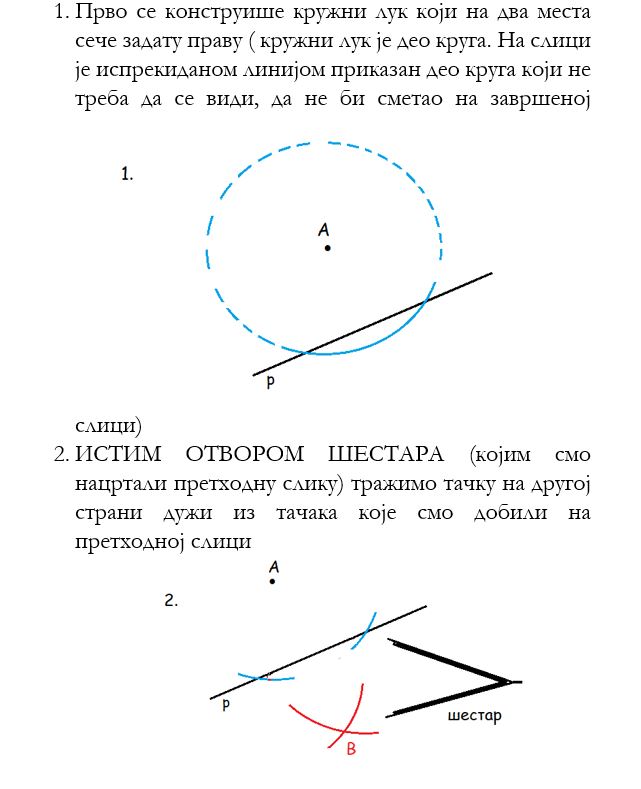
Јуче смо причали о примени симетрале дужи. Што се тиче симетрале угла, она нам је најчешће од к0ристи приликом конструкција појединих углова: нпр, ако нам је потребан угао од 30 степени, ми прво морамо да конструишемо угао од 60 степени, па да га симетралом поделимо на два; угао од 45 степени је половина угла од 90, 15 је пола од 30 итд...

Домаћи задатак: 

подсетити се конструкција углова од 60 и 90 степени, а затим помоћу симетрала, конструисати угао од 45 и 15 степени.

 

 

 

 

Уторак, 26.мај

час 139.

 Петаци, питате ме коју тему ћу проверавати. Већ сам то написао на овом блогу: градиво које смо радили у задња 2 и по месеца. Ви сте на реду када завршим са седмим и шестим разредом, а то је највероватније почетак идуће недеље.

 

 

 

 

 

 

 

Понедељк, 25.мај

час 138.

 

 

 

 

 

 

 

 

 

четвртак, 21.мај 2020.

час 136.

 

 

 

 

 

 

 

среда 20.мај. 2020

час 135.    ОБАВЕШТЕЊЕ ЈЕ ИСПОД ЛЕКЦИЈЕ

 

 

 

 

 

 

 

 

 

 

уторак, 19.мај

час 134.

 

 

 

 

 

 

 

 

 

 

 понедељак, 18.мај 2020.

час 133.

 

 

 

 

 

 

 

 

 

Четвртак 14.мај 2020.

час 132.

 

 

 

 

 

 

 

 Среда, 13.мај 2020.

час 131.

 

 

Уторак, 12.мај 2020.

час 130.

 

 

 

 

 

 

ПОНЕДЕЉАК, 11.МАЈ

 Час 127-129

 

 

 

 

 

 

 субота 9.мај 2020.

час 126.

 

ТВ час, НЕЈЕДНАЧИНЕ

 

 

 

 

петак, 8 мај 2020

час 125.

СЛОЖЕНИЈЕ ЈЕДНАЧИНЕ 

 

Данас вам задајем три текстуална задатка. Они су, као по правилу, кад су у питању једначине (и неједначине) прилично прости за решавање. главни "проблем" у њима је правилно поставити задатак, а то ћете урадити правилно само ако сте задатак потпуно разумели.

 

Пример: Милица је замислила један број, па га увећала 2,5 пута. Затим је од тако добијеног производа одузела 9,8 и добила  је 7,7. Који је број Милица замислила?

 

Решење: Не знамо који је то број, па ћемо га обелижити са х.  Тај број је увећала 2,5 пута: то значи да га је помножила са 2,5. Од производа (2,5 ∙ х) одузела је 9,8 (значи минус 9,8) и добила (једнако) 7,7.

Све то изгледа овако:

2,5 ∙ х - 9,8 = 7,7

просто, зар не?

ваш домаћи су задаци 175 и 178 из збирке.

Додатни задатак. стр 185, задатак185

 

 

 

 

 

 

 

 

 четвртак, 7.мај 2020.

час 124.

 

Среда, 6.мај 2020

123. час

Уторак, 5.мај 2020.

122. час

 

Данашња тема иста као и јучерашња:

БРОЈЕВНИ ИЗРАЗИ

други део 

настављамо са вежбањем:

треба да урадите задатке који се налазе на страни 180 у Збирци.

123. под а, б, в

124. под г

То је ваш домаћи задатак.

Додатни задатак:  

182 стр, зад. 153

 

 

 

 

 

 

Понедељак, 4. мај 2020.

час 121

 

 

 

 

 

Среда, 29.април 2020.

час 120.

Драги петаци, приметили сте да сам прегледао и оценио ваше радове, као и да сам сваком од вас послао образложење и коментар за урађене задатке. Ваши радови су прилично премашили моја очекивања, тако да сам, на основу претходног искуства и начина решавања дошао до закључка да су неки од вас радили потпуно самостално а неки мање самостално. Ипак, ничије резултате нећу да умањујем, тако да , на основу урађеног, могу да закључим да је ова област успешно савладана, и то са врло добрим успехом, а то ме нарочито радује  јер ће нам баш ова област бити јако заступљена у градиву за шести разред.

 

 Поред сумативне оцене свако од вас је добио и формативну оцену активности, другу за овај месец, а дао сам и оцене из Информатике.

Данашња наставна јединица је:

СВОЈСТВА МНОЖЕЊА РАЗЛОМАКА, БРОЈЕВНИ ИЗРАЗИ

 

Множење разломака је комунитативно (подсети се!)

за све разломке важи:

a ∙ b = b ∙ a

 

 

Множење разломака је асоцијативно (подсети се!)

за све разломке важи:

(a ∙ b) ∙ c = a ∙ (b ∙ c)

Нулом се не дели!

 

 

Множење је дистрибутивно према сабирању (веома важно!!)

a ∙ (b + c) = a∙b + a∙c

Домаћи задатак: збирка, страна 178, задаци 101 и 102.

Напомена: у задацима се не тражи да редом рачунате, већ да применом ових правила уредите изразе тако да можете бројеве да скратите и на тај начин знатно смањите рачунање.

 

 

 

 

 

 

 

 

 

Уторак, 28.април 2020.

час 119.

Драги петаци, данас сте радили проверу. Било је неких техничких потешкоћа, вероватно због непотпуне компатибилности наших уређаја, система и апликација. Ипак смо све успели да завршимо у року. задатке ћу прегледати у току ове недеље, када ћете бити и оцењени. Свако од вас ће добити мејл са образложењем оцене.

 

 На ТВ учионици данас је лекција 

ДЕЉЕЊЕ РАЗЛОМАКА

утврђивање

 

Ми смо ту лекцију радили, али ви обавезно треба да испратите све што се емитује на ТВ учионици.

Данас неће бити домаћих задатака јер сте радили проверу. Сутра настављамо.

 

 

 

 

 

 

 

 Понедељак 27. април 2020.

час 118.

 

 

МНОЖЕЊЕ РАЗЛОМАКА

Разломци се множе тако што се помножи бројилац са бројиоцем и именилац са имениоцем:

 Разломци се деле тако што дељеник препишемо, делилац напишемо у облику његове реципрочне вредности и онда множимо.

Кад завршимо и множење и дељење погледамо да ли добијени разломак може да се скрати и да ли може да се претвори у мешовити број. Видимо:

 

Разломке сабирамо и одузимамо само ако имају исте имениоце, тако што именилац препишемо а бројиоце саберемо или одузмемо. 

 

 

Ако немају исте имениоце, разломке морамо проширити да добијемо заједнички именилац:

 

  Сутра је, по договору, писмени задатак. Поновите и рачунске операције са децималним бројевима, као и једначине и неједначине у вези са сабирањем и одузимањем. За сваког од вас је спремљен задатак који ћете добити у 12 сати. На задатку је кратко упутство, прочитајте га и поступите по њему. Имате довољно времена, читавих пола сата више него у школи. Прочитајте сваки задатак и више пута ако треба, да би вам било јасно шта треба да урадите.

 

 

 

 

 

Четвртак 23.април 2020.

час 117.

 

Добио сам неколико мејлова са домаћим задацима, али само једно обавештење да сте прочитали и разумели обавештење о писменом задатку. Зато га постављам поново:

У уторак 28.априла, радићете писмени задатак. Тога дана ће свако од вас у 12 сати добити задатке које треба да уради, фотографише и те фотографије пошаље на мој мејл најкасније до 13сати и петнаест минута. Задатке ћете добити на мејл адресе са којих сте ми се до сада јављали. Задаци ће бити из области сабирања, одузимања, множења и дељења разломака. Свако од вас ће имати задатке исте тежине али са другачијим подацима.

Напомињем да задатке који пристигну после задатог рока нећу узимати у обзир. Молим да овај писмени задатак схватите најозбиљније, јер ћу вам на основу њега дати једну од оцена. АКО ВАМ ЈЕ БИЛО ШТА НЕЈАСНО у вези овог обавештења ПИТАЈТЕ НА ВРЕМЕ!! ТАКОЂЕ, ДА МИ СЕ СВИ ЈАВИТЕ ДО ПЕТКА, ДА СТЕ ПРОЧИТАЛИ И РАЗУМЕЛИ ОБАВЕШТЕЊЕ!!

 

 Данашња наставна јединица се односи на

 

ДЕЉЕЊЕ РАЗЛОМАКА

утврђивање

 

Поново прочитајте објашњења и правила са претходног часа!

 

За домаћи урадите задатке из Збирке, страна  171, задатак 45 од е до к и 46 задатак од е до и. 

Додатни задатак: стр 178, задатак 104

 

Среда, 22.април 2020.

час 116. 

 ВАЖНО!!ВАЖНО!!ВАЖНО!!

ВАЖНО!!ВАЖНО!!

Драги петаци, у уторак 28.априла, радићете писмени задатак. Тога дана ће свако од вас у 12 сати добити задатке које треба да уради, фотографише и фотографије пошаље на мој мејл најкасније до 13сати и петнаест минута. Задатке ћете добити на мејл адресе са којих сте ми се до сада јављали. Задаци ће бити из области сабирања, одузимања, множења и дељења разломака. Свако од вас ће имати задатке исте тежине али са другачијим подацима.

Напомињем да задатке који пристигну после задатог рока нећу узимати у обзир. Молим да овај писмени задатак схватите најозбиљније, јер ћу вам на основу њега дати једну од оцена. АКО ВАМ ЈЕ БИЛО ШТА НЕЈАСНО у вези овог обавештења ПИТАЈТЕ НА ВРЕМЕ!! ТАКОЂЕ, ДА МИ СЕ СВИ ЈАВИТЕ ДО ПЕТКА, ДА СТЕ ПРОЧИТАЛИ И РАЗУМЕЛИ ОБАВЕШТЕЊЕ!!

 

 Данашња наставна јединица се односи на

 

ДЕЉЕЊЕ РАЗЛОМАКА

 

Дељење разломака се врши на следећи начин: 

1. Дељеник препишемо

2. Напишемо знак за множење

3. делилац напишемо у реципрочном облику

4. множимо по правилу за множење: бројилац пута бројилац, именилац пута именилац 

Пример:

 

 

 

 Подсећам вас да је РЕЦИПРОЧНА ВРЕДНОСТ БРОЈ КОЈИМ СЕ МНОЖИ НЕКИ ДРУГИ БРОЈ ДА БИ СЕ ДОБИЛА ЈЕДИНИЦА.

На слици испод видите пример четири разломака и њихових реципрочних вредности

 

 

 а производ неког броја и реципрочне вредности тог броја је увек 1

 

 Као што видите, реципрочну вредност неког разломка лако добијемо тако што "обрнемо" разломак, тј. заменимо места бројиоцу и имениоцу.

 

 Дељење разломка ЦЕЛИМ БРОЈЕМ се врши тако што се целом броју допише јединица у именилац и онда дели по правилу за дељење:

 ДОМАЋИ ЗАДАТАК: Збирка, страна 171, задатак 45 а-ђ

46 задатак а-ђ. 

НАПОМЕНА: ако у дељењу учествују мешовити бројеви МОРАМО ИХ претворити у разломке, и онда делити.

 

 

 Уторак, 21.април 2020

час 115

 

МНОЖЕЊЕ И ДЕЉЕЊЕ ДЕЦИМАЛНИХ БРОЈЕВА 

утврђивање

 

ваш данашњи задатак:

 

 

 

 

 

 

 

 

 

 

четвртак, 16. април 2020.

час 114

 

 

 

 

 

 

 

 

 

 

 

 

 

среда, 15.април 2020.

час 113

 

 

ДЕЉЕЊЕ ДЕЦИМАЛНИХ БРОЈЕВА

 

 

АКО ДВА ДЕЦИМАЛНА БРОЈА ИМАЈУ ЈЕДНАК БРОЈ ДЕЦИМАЛА, ОБРИШЕМО ЗАРЕЗЕ И ДЕЛИМО ИХ КАО ЦЕЛЕ БРОЈЕВЕ. АКО НЕМАЈУ, ДОПИСУЈЕМО НУЛЕ ОНОМ БРОЈУ КОЈИ ИМА МАЊЕ ДЕЦИМАЛНИХ МЕСТА, ПА ОПЕТ БРИШЕМО ЗАРЕЗЕ. 

И данас је час утврђивања градива.

Ваши задаци за вежбање и домаћи су:

 

 

 

 

 

   

уторак, 14.април 2020.

час 112

 

 

Драги петаци, после првих двадесетак дана добили сте и прве оцене активности. Већина вас је била и остала  врло активна, и сходно томе и добро оцењена. Разумљиво је да нисмо могли сви одмах и у истој мери да се пребацимо на овакав начин наставе, из много разлога који су мање или више оправдани. Ускоро ће бити почето и са бројчаним оцењивањем пошто смо неке области завршили. Ваше је да пратите ТВ учионицу, и наставу коју држим преко овог блога, и да се потрудите најбоље што можете у овом тренутку. По задацима које добијам видим да напредујете, и то је за сваку похвалу. Ипак, још увек нисам са свима успоставио контакт, јер очигледно да неки родитељи и ученици не схватају у довољној мери озбиљност ситуације у којој се налазима и начина на који покушавамо да превазиђемо ту ситуацију.

 

 

Данашња наставна јединица је 

 

 

ДЕЉЕЊЕ ДЕЦИМАЛНИХ БРОЈЕВА

 

и у њој настављамо са задацима. По оним задацима које сте послали видим да сте усвојили начин дељења. Ипак , још једном истичем правило:

 

 

 АКО ДВА ДЕЦИМАЛНА БРОЈА ИМАЈУ ЈЕДНАК БРОЈ ДЕЦИМАЛА, ОБРИШЕМО ЗАРЕЗЕ И ДЕЛИМО ИХ КАО ЦЕЛЕ БРОЈЕВЕ. АКО НЕМАЈУ, ДОПИСУЈЕМО НУЛЕ ОНОМ БРОЈУ КОЈИ ИМА МАЊЕ ДЕЦИМАЛНИХ МЕСТА, ПА ОПЕТ БРИШЕМО ЗАРЕЗЕ.

 

Као у следећем примеру: дељеник има три децимале а делилац две. Допишемо нулу делиоцу, сада оба броја имају исти број децимала. обришемо зарезе и делимо два цела броја.

 

 

 Пример је мало смешно исписан, још се нисам навикао да пишем на табли, али нећете замерити.

 

ДОМАЋИ: 

 ДОДАТНИ ЗАДАЦИ:  Збирка, 176стр, задатак 95

 

понедељак, 13.април 2020.

час 111

 

 

Данас је на ТВ учионици а и на нашем блогу на реду 

ДЕЉЕЊЕ ДЕЦИМАЛНОГ БРОЈА ПРИРОДНИМ БРОЈЕМ

 

 подсетимо се:

ДЕЉЕЊЕ ДЕЦИМАЛНОГ БРОЈА ДЕКАДНОМ ЈЕДИНИЦОМ се врши тако што се децимални зарез (запета) помера У ЛЕВО ЗА ОНОЛИКО МЕСТА КОЛИКО НУЛА ИМА ДЕКАДНА ЈЕДИНИЦА КОЈОМ ДЕЛИМО!

 

Покажимо на примеру:

12, 453  :  10  =  1,2453

12, 453  ∙  100  =  0,12453

12, 453  ∙  1000 =  0,012453

Сада ћемо, користећи примере, показати правило за дељење децималних бројева, које важи и када делимо природним бројем.

 

 

 

ПРАВИЛО ДЕЉЕЊА ЈЕ:

 АКО ДВА ДЕЦИМАЛНА БРОЈА ИМАЈУ ЈЕДНАК БРОЈ ДЕЦИМАЛА, ОБРИШЕМО ЗАРЕЗЕ И ДЕЛИМО ИХ КАО ЦЕЛЕ БРОЈЕВЕ

 10,2 : 5,1 =  102 : 51

3, 24 : 4, 11 = 324 : 411

26, 765 : 5,234 = 26765 : 5234

пример 1: дељење природним бројем

32,2 : 2 = ?

видимо да дељеник има једну децималу а делилац нема. Ако броју 2 допишемо нулу као децималу онда имамо 

 

32,2 : 2,0 =

Видимо да оба броја имају по једну децималу, па применимо правило дељења: 

322 : 20 = 16,1

                            20

                            122

                            120

                                20

                                20 

                                ==

 

пример 2: дељење децималним бројем када бројеви немају исти број децимала:

52,1 : 26,05 =

видимо да делилац има једну децималу више од дељеника: зато дељенику дописујемо нулу као другу децималу и имамо:

52,11 : 26,05 = 

примењујемо правило и бришемо зарезе, па добијемо:

5211 : 2605 = 2 

 

И то је то!!! поновимо правило:

 АКО ДВА ДЕЦИМАЛНА БРОЈА ИМАЈУ ЈЕДНАК БРОЈ ДЕЦИМАЛА, ОБРИШЕМО ЗАРЕЗЕ И ДЕЛИМО ИХ КАО ЦЕЛЕ БРОЈЕВЕ. АКО НЕМАЈУ, ДОПИСУЈЕМО НУЛЕ ОНОМ БРОЈУ КОЈИ ИМА МАЊЕ ДЕЦИМАЛНИХ МЕСТА, ПА ОПЕТ БРИШЕМО ЗАРЕЗЕ.

 

 

 Домаћи задатак: Збирка, страна 174, задатак 69 под а,б,в

и 175 страна, задатак 70 а-ј.

Додатни задатак: 176, зад. 88 и 90.

 

 

 

 

петак, 10. април 2020.

час 110.

Драги петаци, и данас ћемо радити

МНОЖЕЊЕ ДЕЦИМАЛНИХ БРОЈЕВА

утврђивање

поновимо прво правила која смо научили:

МНОЖЕЊЕ ДЕЦИМАЛНОГ БРОЈА ДЕКАДНОМ ЈЕДИНИЦОМ се врши тако што се децимални зарез (запета) помера У ДЕСНО ЗА ОНОЛИКО МЕСТА КОЛИКО НУЛА ИМА ДЕКАДНА ЈЕДИНИЦА КОЈОМ МНОЖИМО!

ДЕЉЕЊЕ ДЕЦИМАЛНОГ БРОЈА ДЕКАДНОМ ЈЕДИНИЦОМ се врши тако што се децимални зарез (запета) помера У ЛЕВО ЗА ОНОЛИКО МЕСТА КОЛИКО НУЛА ИМА ДЕКАДНА ЈЕДИНИЦА КОЈОМ ДЕЛИМО!

МНОЖЕЊЕ ДВА ДЕЦИМАЛНА БРОЈА СЕ ОБАВЉА КАО ДА НЕМА ДЕЦИМАЛНИХ ЗАРЕЗА, АЛИ СЕ У ПРОИЗВОДУ МОРА ОДВОЈИТИ ОНОЛИКО ДЕЦИМАЛНИХ МЕСТА КОЛИКО ИХ УКУПНО ИМА У ЧИНИОЦИМА.

Тако, ако у операцији множења учествује више чиниоца, рачунају се места сваког од њих:

0,01 ∙ 0,001 ∙ 0,1 ∙ 0,0001 =  0,0000000001


за домаћи задатак још мало вежбања:

3,27 ∙ 1,42 =
11, 6 ∙ 2,45 =
25, 772 ∙ 3,1 =
0,002 ∙ 431 =
25 ∙ 12,63 =
0,1 ∙ 0,2 ∙ 0,3 =
0,01 ∙ 0,2 ∙ 0,003 =

додатни задаци: Збирка, страна 175, задаци 81 и 87.
ДОДАТНИ ЗАДАЦИ НИСУ ОБАВЕЗНИ.

 

четвртак, 9.април 2020.

час 109

 

Данашња наставна јединица је:

МНОЖЕЊЕ ДЕЦИМАЛНИХ БРОЈЕВА

утврђивање

Ово су задаци за вежбање, и уједно ваш домаћи задатак:

 

 

 

 

 

 

 

 

Среда, 8.април 2020.

час 108

 

 

Драги петаци, од данас ћу, осим обавезног задатка за домаћи, давати и предлог задатка вишег нивоа. Тај задатак нисте у обавези да урадите, он је изазов за оне ученике који желе да постигну боље резултате.

Данашња наставна јединица је:

МНОЖЕЊЕ ДЕЦИМАЛНИХ БРОЈЕВА

 

Видели смо како се множе децимални бројеви декадним јединицама. подсетимо се:

 

МНОЖЕЊЕ ДЕЦИМАЛНОГ БРОЈА ДЕКАДНОМ ЈЕДИНИЦОМ се врши тако што се децимални зарез (запета) помера У ДЕСНО ЗА ОНОЛИКО МЕСТА КОЛИКО НУЛА ИМА ДЕКАДНА ЈЕДИНИЦА КОЈОМ МНОЖИМО!

 

 

Што се тиче множења два "обична" децимална броја поступак је следећи, а објаснићу га кроз следећи пример:

као што видите, није много тешко. Провежбајте следеће задатке:

Домаћи задатак: страна 174 у Збирци, задатак 65 од а до м

Додатни задатак: исто, од м до љ.

 

 

 

 

 

Понедељак, 6.април 2020.

час 106 и 107.

Драги петаци, ево новог распореда на ТВ учионици.

Данас ћемо да поновимо све оно најважније што смо научили о сабирању и одузимању разломака, а затим да кренемо на нову наставну јединицу која се зове

МНОЖЕЊЕ И ДЕЉЕЊЕ ДЕЦИМАЛНОГ БРОЈА ДЕКАДНОМ ЈЕДИНИЦОМ.

 

 

 

 Подсетимо се прво најважнијих правила у вези са сабирањем и одузимањем разломака и децималних бројева.

 

ДЕЦИМАЛНЕ БРОЈЕВЕ САБИРАМО И ОДУЗИМАМО ПОТПИСИВАЊЕМ.

РАЗЛОМКЕ САБИРАМО И ОДУЗИМАМО САМО АКО ИМАЈУ ИСТИ ИМЕНИЛАЦ И ТО ТАКО ШТО ИМЕНИЛАЦ ПРЕПИШЕМО, А БРОЈИОЦЕ САБЕРЕМО ИЛИ ОДУЗМЕМО.

АКО РАЗЛОМЦИ НЕМАЈУ ИСТЕ ИМЕНИОЦЕ НЕОПХОДНО ЈЕ ДА ИХ ПРОШИРИМО ДО ИСТОГ ИМЕНИОЦА.

ПРИЛИКОМ ИЗРАЧУНАВАЊА БРОЈЕВНИХ ИЗРАЗА МОРА СЕ ВОДИТИ РАЧУНА ДА ПРВЕНСТВО У РАЧУНАЊУ ИМАЈУ ИЗРАЗИ У ЗАГРАДАМА, МНОЖЕЊЕ И ДЕЉЕЊЕ ПА ТЕК НА КРАЈУ САБИРАЊЕ И ОДУЗИМАЊЕ.

 АКО У БРОЈЕВНОМ ИЗРАЗУ КОЈИ РЕШАВАМО ИМАМО БРОЈЕВЕ КОЈИ ПРИПАДАЈУ РАЗЛИЧИТИМ ВРСТАМА РАЗЛОМАКА (ДЕЦИМАЛНИ БРОЈ, МЕШОВИТИ БРОЈ, ЦЕО БРОЈ, РАЗЛОМАК) НЕОПХОДНО ЈЕ СВЕ БРОЈЕВЕ ПРЕТВОРИТИ ИЛИ У РАЗЛОМКЕ ИЛИ У ДЕЦИМАЛНЕ БРОЈЕВЕ, ПА ОНДА РЕШАВАТИ.

ОПЕРАЦИЈА САБИРАЊА ЈЕ КОМУТАТИВНА И АСОЦИЈАТИВНА (ОДУЗИМАЊЕ НИЈЕ!!!)

 

То би била правила која смо све време понављали и која би требало увек да имамо на уму, А сада ћемо објаснити како се децимални бројеви множе и деле декадним јединицама. 

Подсетимо се: декадне јединице су 10, 100, 1000, 10000.... као што видите, свака од њих почиње бројем 1, а разликују се по броју нула иза те јединице (број 20 није декадна јединица, јер не почиње бројем 1!!)

Покажимо на примеру:

12, 453  ∙  10  =  124,53

12, 453  ∙  100  =  1245,3

12, 453  ∙  1000 =  12453

Примећујете да су цифре у производу увек исте, само се разликује место на коме се налази зарез. Правило је следеће:

МНОЖЕЊЕ ДЕЦИМАЛНОГ БРОЈА ДЕКАДНОМ ЈЕДИНИЦОМ се врши тако што се децимални зарез (запета) помера У ДЕСНО ЗА ОНОЛИКО МЕСТА КОЛИКО НУЛА ИМА ДЕКАДНА ЈЕДИНИЦА КОЈОМ МНОЖИМО!

Зар није лако? Ево још примера:   

123,456789  ∙  1000 =  1234567,89

5, 2  ∙ 10  =  52

5, 2  ∙ 100  =  520

5, 2  ∙ 1000  =  5200

5, 2  ∙ 10000  =  52000

 

Кад се тако лако множи, вероватно се и лако дели, зар не?

Тако је. 

ДЕЉЕЊЕ ДЕЦИМАЛНОГ БРОЈА ДЕКАДНОМ ЈЕДИНИЦОМ се врши тако што се децимални зарез (запета) помера У ЛЕВО ЗА ОНОЛИКО МЕСТА КОЛИКО НУЛА ИМА ДЕКАДНА ЈЕДИНИЦА КОЈОМ ДЕЛИМО!

 

Покажимо на примеру:

12, 453  :  10  =  1,2453

12, 453  ∙  100  =  0,12453

12, 453  ∙  1000 =  0,012453

Домаћи задатак: Збирка, страна 173 задатак 61 а-м и стр 174 зад 70, исто од а до м

Четвртак, 2.април 2020.

105.час.

Драги петаци, од данас изједначавамо наставне јединице са ТВ учионицом. Данашња јединица је била, а ако је неко од вас није погледао може то да уради на  линку

https://rtsplaneta.rs/video/show/1375325/

ЈЕДНАЧИНЕ И НЕЈЕДНАЧИНЕ 1. ПРИМЕНА

Примена једначина и неједначина је у решавању проблемских задатака. Сваки такав задатак је задат текстуално, речима, а ми треба да тај запис претворимо у математички запис, и да тако добијен израз израчунамо. То и јесте главни проблем: за само решавање користимо методе које смо учили (израчунавање непознатог сабирка, умањеника или умањиоца).

Пример из вашег збирке: 

Два молера су за један дан окречила једну петнаестину зграде. Ако је један окречио једну двадесетину, колико је окречио други?

Решење:  увек размишљљамо на следећи начин: шта треба да израчунамо? Треба да израчунамо колико је окречио други молер! То је оно што се тражи и што ћемо представити непознатом х. 

Када се сабере колико је један молер урадио (а то је једна двадесетина) са оним колико је други молер урадио (а то је х) добиће се једна петнаестина. 

ето то је наша једначина, само треба да је математички запишемо, а затим решимо: 

Ваш ДОМАЋИ задатак је да текстуални задатак бр.169 на страни 158 ваше збирке запишете као једначину, и решите ту једначину.