Петак, 29.мај 2020.
ВАЖНО ОБАВЕШТЕЊЕ!!
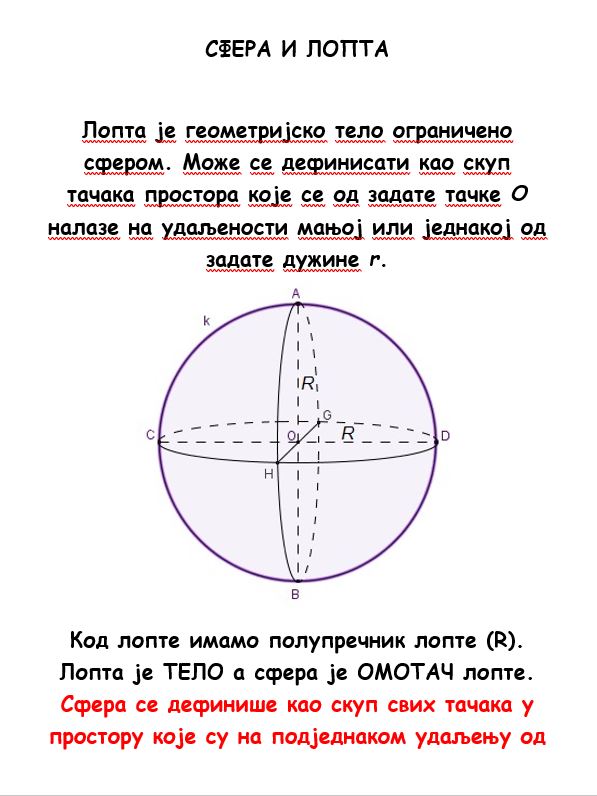
драги осмаци, дошли смо до краја наставног плана и програма. У овој несвакидашњој ситуацији смо сви имали изазове на које нисмо навикли, али мислим да смо се добро снашли. Комуницирали смо редовно у мањој или већој мери, а и знате да сматрам да сте се сви трудили. Имали смо провере и писмено и усмено, а и редовно сам пратио вашу активност као и тачност и уредност задатака које сте решавали. На основу тога, у нашем директном разговору преко Вибера, свако од вас је, са моје стране, добио предлог закључне оцене. Сви сте се сложили, али ми је неопходна и ваша потврда преко мејла. ПОШАЉИТЕ МИ МЕЈЛ У КОМЕ СЕ ИЗЈАШЊАВАТЕ ДА ЛИ СТЕ ЗАДОВОЉНИ ПРЕДЛОГОМ ЗАКЉУЧНЕ ОЦЕНЕ! Дакле, или "Обавештен (обавештена) сам и сагласан сам са Вашим предлогом закључне оцене" или "Обавештен (обавештена) сам и НИСАМ сагласан сам са Вашим предлогом закључне оцене". У овом другом случају ћете, као и што сам вам рекао приликом саопштавања предлога, моћи да у одређеном термину одговарате за већу оцену (што би било, како претпостављамо, организовано у нашој школи). Наравно, можете тражити додатно одговарање ако сматрате да у вашим досадашњим оценама има елемената за већу оцену. У сваком случају, свакој вашој жељи ћу изаћи у сусрет, зато молим да ме обавестите у најкраћем року.
УТОРАК, 26. мај
136. час
Ево, званично, последњег, 136. часа, који је наставним планом и програмом предвиђен за вас осмаке. Нисмо имали редовне услове, али смо ову годину привели крају. Остаје вам да полажете (прво пробни) завршни испит. У оквиру припрема за тај дан постављаћу вам линкове за ТВ учионицу; пратите ту наставу, јер је велика вероватноћа да ће бити обрађиване области које ће бити заступљене на испиту.
https://mojaskola.rtsplaneta.rs/show/1466771/532/os8-matematika-algebra-i-funkcije-obnavljanje
https://mojaskola.rtsplaneta.rs/show/1468386/532/os8-matematika-algebra-i-funkcije-obnavljanje
четвртак, 21.мај 2020.
час 135.
Среда, 20.мај
час 134.
ОБАВЕШТЕЊЕ ЈЕ ИСПОД ЛЕКЦИЈЕ!!!
Понедељак 18. мај
УОПШТЕ НЕ ПОСЕЋУЈЕТЕ ПРИПРЕМНИ БЛОГ, НА КОМЕ ВАМ РЕДОВНО ПОСТАВЉАМ ТЕСТОВЕ!!!!!
Четвртак, 14.мај
час 131.
уторак, 12.мај 2020.
час 130.
Понедељак, 11.мај 2020 час 129.
Драги осмаци, данас сте радили
писмену проверу. Задаци ће бити прегледани у току недеље, после чега
ћете мејлом добити коментар и обавештење о оцени која ће бити унета у
дневник.
Недеља, 10.мај
час 126.
Петак, 8.мај 2020.
час 125
Среда, 6.мај 2020.
час 124.
понедељак, 4.мај 2020.
час 122-123.
среда, 29. април 2020.
час 120-121.
ЗАПРЕМИНА КУПЕ
Као што смо указивали на аналогију приликом израчунавања запремине ваљка и запремине призме, тако исто можемо урадити поредећи купу и пирамиду:

Општи обрасци запремине пирамиде и купе су исти:
Како је В = пr² следи да је
Домаћи задатак: израчунати запремину купе чија је висина 10 а полупречник 6цм.
Додатни задатак: уџбеник, стр. 147, зад. 2
уторак, 28 април 2020
час 119.
МРЕЖА И ПОВРШИНА КУПЕ
утврђивање
Подсетимо се:
мрежу купе чине круг, који је основица купе и чија се површина израчунава према формули:
B = 𝛑r²
где је r полупречник датог круга
Омотач је у кружни исечак, код кога је полупречник једнак дужини изводнице а дужина кружног лука је једнака ОБИМУ БАЗЕ!!!
M = 𝛑rs
где је r полупречник датог круга а s је дужина изводнице.
Укупна површина купе је збир површина основице (В) и омотача (М) па имамо:
Р = В + М
Р = 𝛑r² + 𝛑rs
Р = 𝛑r(r + s)
Домаћи задатак: збирка, стр 88 задатак 2
Додатни задатак : збирка, стр 87, зад. 3
понедељак 27. април, 2020.
час 117-118
среда, 22. април 2020.
ВАЖНО!!ВАЖНО!!ВАЖНО!!
ВАЖНО!!ВАЖНО!!
Драги шестаци, у понедељак 11. маја, радићете писмени задатак. Тога дана ће свако од вас у 12 сати добити задатке које треба да уради, фотографише и фотографије пошаље на мој мејл најкасније до 13 сати и петнаест минута. Задатке ћете добити на мејл адресе са којих сте ми се до сада јављали. Задаци ће бити из области које смо радили у периоду од другог писменог: Функције, Табеларно и графичко представљање зависних величина, Системи линеарних једначина, Ваљак и Купа. Свако од вас ће имати задатке исте тежине али са другачијим подацима.
Напомињем да задатке који пристигну после задатог рока нећу узимати у обзир. Молим да овај писмени задатак схватите најозбиљније, јер ћу вам на основу њега дати једну од оцена. АКО ВАМ ЈЕ БИЛО ШТА НЕЈАСНО у вези овог обавештења ПИТАЈТЕ НА ВРЕМЕ!! ТАКОЂЕ, ДА МИ СЕ СВИ ЈАВИТЕ ДО ПЕТКА, ДА СТЕ ПРОЧИТАЛИ И РАЗУМЕЛИ ОБАВЕШТЕЊЕ!!
Уторак, 21.април 2020
116. час
Драги осмаци, настављамо... Још двадесет редовних часова, и преостаће нам само припрема за завршни испит. Данашња наставна јединица на ТВ учионици и код нас је
МРЕЖЕ И ПОВРШИНА КУПЕ
Мрежа купе претстављена је на слици испод:
Омотач купе је кружни исечак, обележавамо га словом М
База (основица) купе је круг, обележавамо га са В.
ПОВРШИНА КУПЕ ЈЕ ЗБИР ПОВРШИНА ОСНОВИЦЕ И ОМОТАЧА
P = B + M
Знамо да је површина круга једнака
B = π r²
где је r полупречник базе.
Површина кружног исечка је (седми разред!!)

М = π r²𝝰
360⁰где је r полупречник кружног исечка, а у нашем случају он је исто што и изводница, па можемо написати
М = π 𝐬²𝝰
360⁰
Из седмог разреда такође знамо да се дужина кружног лука (𝑙) рачуна из обрасца
𝑙 = πr𝝰
180⁰
Ако знамо да су, у нашем случају, обим круга (основице, 2πr) и дужина кружног лука омотача (𝑙) исте дужине (јер омотач потпуно обавија круг), као и да је полупречник омотача у ствари изводница 𝑠, можемо израчунати:
P = πr² + πrs
P = πr(r + s)
Домаћи задатак: израчунати површину купе (претходно нацртати мрежу и обележити је) ако је њен полупречник 5цм а изводница 8цм
Додатни задаци: уџбеник, страна 144 задаци 2 и 5
среда, 15.април 2020.
час 115
КУПА, ПОЈАМ И ЕЛЕМЕНТИ
Линк за данашњи час
https://mojaskola.rtsplaneta.rs/show/1397409/532/os8-matematika-kupa-pojam-i-elementi
На слици испод су приказани основни елементи купе.
Основа (база) купе је круг. Омотач чини такозвана КОНУСНА ПОВРШ.
Као и ваљак, и купа спада у ОБРТНА тела.
Њу формира троугао који ротира око једне катете (зашто не и хипотенузе? Размислите).
Видимо да ВИСИНА КУПЕ, ПОЛУПРЕЧНИК ОСНОВЕ и ИЗВОДНИЦА граде правоугли троугао.
Задатак за ДОМАЋИ су везани управо за тај троугао. Приликом решавања ћете користити ПИТАГОРИНУ ТЕОРЕМУ:
уџбеник, страна 138 задатак 1.
уторак, 14.април 2020.
час 114
Драги осмаци, после првих двадесетак дана добили сте и прве оцене активности. Већина вас је била и остала врло активна, и сходно томе и добро оцењена. Разумљиво је да нисмо могли сви одмах и у истој мери да се пребацимо на овакав начин наставе, из много разлога који су мање или више оправдани. Ускоро ће бити почето и са бројчаним оцењивањем пошто смо неке области завршили. Ваше је да пратите ТВ учионицу, и наставу коју држим преко овог блога, и да се потрудите најбоље што можете у овом тренутку.
Прелазимо на ново геометријско тело које се зове
КУПА

На слици изнад су приказане две купе. Лево је ПРАВА а десно је КОСА купа. Нас ће занимати само права купа.
Као што има доста аналогија и сличности између ваљка и призме, тако их има и између купе и пирамиде.

Ваш задатак је да одгледате ТВ лекцију, прочитате лекцију из вашег уџбеника и НАЦРТАТЕ КУПУ И ОБЕЛЕЖИТЕ СВЕ ЊЕНЕ ЕЛЕМЕНТЕ!!
понедељак, 13 април 2020.
час 113
И данашњи час је на ТВ учионици, а и на блогу, везан за ваљак као геометријско тело.
За прве две недеље сам оценио вашу активност.
Један број вас се редовно јављао и слао задатке са задацима али има и оних који су се јављали врло ретко па и никако. Подсећам вас да је то за сада једини начин да пратим ваш рад и зато немојте све то олако схватати.
ВАЉАК
систематизација
ВАЉАК је ГЕОМЕТРИЈСКО ТЕЛО, врло слично призми по
многим својим особинама.
Елементи ваљка су:
има
две основице. Свака има свој полупречник (на слици изнад, дуж ВС, означена малим r)
има
висину (на слици изнад дуж АВ, означена великим Н)
ваљак
нема ивице, има ИЗВОДНИЦУ. Она је једнака висини, на слици је приказана
као дуж CD и обележена малим словом s.
ПОВРШИНА
ВАЉКА ЈЕДНАКА ЈЕ ЗБИРУ ПОВРШИНА ОСНОВИЦА(В) И ОМОТАЧА(М).
В
= πr²
Омотач
је правоугаоник, коме је једна страна ВИСИНА(Н) ваљка а друга страна ОБИМ
ОСНОВИЦЕ( 2πr)
па је
наш коначни образац:
P
= 2πr² + 2πrН
P = 2πr
( r + Н)
запремина ваљка је једнака производу површине основице и висине ваљка.
знамо да је основица ваљка круг а површина круга се рачуна по формули
В = πr²
тако да је коначно
V = πr²·H
Домаћи задатак: Уџбеник, страна 136, задатак 2 и 5
Додатни задатак : уџбеник, страна 136 задаци 4 и 7
четвртак, 9.април 2020
час 112
ПОВРШИНА И ЗАПРЕМИНА ВАЉКА
утврђивање
Задатак1. Правоугаоник чија је једна страница 9 cm и дијагонала 15 cm ротира око
мање странице. Израчунај површину и запремину тако насталог тела.
Ми не знамо која је страница од 9 цм, да ли је она дужа или краћа. То ћемо утврдити из правоуглог троугла који граде дијагонала и странице правоугаоника. Дијагонала је хипотенуза па мора да важи:
15² = 9² + х²
х² = 15² - 9²
х² = 225 - 81
х² = 144
х = √144
х = 12
дакле, дужа страница је 12, а краћа 9 па тело које настаје изгледа овако:
Добијамо ваљак полупречника 12 и висине 8.
пдсетимо се:
V = πr²h
V = π ∙ 12² ∙9
V = π ∙ 144 ∙9
V = π ∙ 9² ∙12
V = 1296 πcm³
P = 2 ∙ π r ∙ (r + h)
P = 2 ∙ π 12 ∙ (12 + 9)
P = 24 π ∙ 21
P = 504 π cm²
Домаћи: ИСТИ ЗАДАТАК, САМО ШТО ЈЕ РОТАЦИЈА ОКО СИМЕТРАЛЕ ВЕЋЕ СТРАНЕ.
Додатни задатак (необавезно):
1.Израчунати површину ваљка чија је висина 8cm, а обим његове основе 4π cm.
2.Површина ваљка је 48 π cm2, а површина његовог омотача је 30 π cm2. Израчунати површину осног пресека тог ваљка.
Среда, 8.април 2020.
час 111
ЗАПРЕМИНА ВАЉКА
утврђивање
Подсетимо се: запремина ваљка се израчунава према формули
V = πr²·H
Задатак: површина ваљка је 48π cm², а површина његовог омотача 30π cm². Израчунати његову запремину.
Решење:

пишемо задате и тражене величине: није нам задат ни полупречник ни висина, али имамо површину (Р) ваљка и површину омотача (М)
Р = 48π cm²
М =30π cm²
V = ?
Рекли смо: да би применили образац за запремину МОРАМО ДА ОДРЕДИМО полупречник и висину ваљка.
у једначини за површину
заменимо оно што знамо, а то су Р и М
48π
= 2B + 30π
и добијамо
48π - 30π = 2В
одатле
2В = 18π
В = 18 π : 2
В = 9