МАТЕМАТИКА 7.РАЗРЕД

 

Недеља, 7.јун 2020.

ОБАВЕШТЕЊЕ:

 

Због седнице која је заказана за уторак у 9 сати, обавештавам ученике који желе да одговарају у циљу поправљања оцене, да време испитивања померам за 8 сати. Све остало остаје исто.

 

 

 

 

 Четвртак, 4.јун 2020.

 

 

 

 

 

 

 

 петак, 29. мај

 

Драги седмаци, данас је последњи час на ТВ учионици.

Према одлуци Министарства, настава на даљину траје још две недеље, и то време ћемо искористити за обнављање и утврђивање градива које смо прешли у овом разреду.

 НАСТАВИТЕ ДА ПРАТИТЕ ОВАЈ БЛОГ, ЈЕР ВАС ОЧЕКУЈУ ВАЖНА ОБАВЕШТЕЊА. Такође ћу вам постављати и лекције које треба да обновите.

За почетак, обновите за викенд лекцију"Квадратни корен", која се налази на почетку вашег уџбеника.

Домаћи задатак: Уџбеник, страна 14, задаци 1, 2 и 4.

 

 

 

 

 

 

 

 

 

 

Среда, 27.мај

час 140. 

 

Данас је био час провере знања, скоро сви сте одговарали и добили по оцену. Свима сам рекао, али ћу да поновим, да ћете почетком идуће недеље сви добити још по једну оцену за активност, коју ћу давати на основу вашег рада у протеклом периоду, при чему мислим на број радова које сте ми послали и заинтересованост коју сте показали у комуникацији са мном. 

Када вам будем дао ту последњу оцену, свакоме од вас ћу послати слику ваше странице из електронског дневника, која показује ваше оцене и активности. Видећете и предлог ваше закључне оцене.

Наставите да пратите овај блог и ТВ учионицу.

 

 

 

 

 

 

Уторак, 26.мај

час 139.

ЈОШ УВЕК МИ НИСТЕ СВИ ПОСЛАЛИ БРОЈЕВЕ ТЕЛЕФОНА. ОНИМА КОЈЕ НЕ БУДЕМ МОГАО ДА ИСПИТАМ НЕЋУ МОЋИ ДА ЗАКЉУЧИМ ОЦЕНУ!!

НЕКИ ВАС ДУГО НИСУ СЛАЛИ ЗАДАТКЕ И ВРЛО СУ НЕАКТИВНИ, И ПОРЕД МОЈИХ УПОЗОРЕЊА!!!

 

 

 

 

 

 

Понедељак, 25 мај, час 138.

 

 

 

 

 

 

Четвртак, 21.мај 2020.

час 136.

 

И данас делимо дужи на једнаке делове.

Ваш задатак (домаћи, наравно) је да поделите странице једнакостраничног троугла (а = 9цм) у односу 3 : 4 : 5

 

 

 

 

 

 

Среда, 20.мај 2020.

час 134.  

 

ОБАВЕШТЕЊЕ ЈЕ ИСПОД ЛЕКЦИЈЕ!!!

 

   

 

 

 

 

 

 

УТОРАК, 19.мај

час 133.

 

 

 

Понедељак, 18.мај 2020.

 

 

 

 

 

Четвртак, 14.мај 2020.

час 131.

 

 На данашњој ТВ учионици је одржан час под називом

 

 

МАТЕМАТИКА И СПОРТ,

вежбање

 

 Ако нисте одгледали час, то вам је домаћи задатак. Час се налази на линку:

 https://mojaskola.rtsplaneta.rs/show/1451129/531/os7-matematika-matematika-i-sport-vezbanje

 

 

 

 

 

Уторак, 12. мај 2020.

час 130.

 

 

 

 

 

 

 

 

 

ПОНЕДЕЉАК, 11.мај 2020

час 127-129. 

 

 

 

 

 

петак, 8.мај 2020.

час 125-126

 

 

 

 

 

 

 

 

СРЕДА 6,МАЈ 2020

ЧАС 124.

 

 

ПОВРШИНА КРУГА

утврђивање 

 

Ваш данашњи задатак је да урадите примере из Уџбеника, страна 144 пример 1 и пример 2. Такође одговорити на питања на страни 145.

 

 

 

 

 

 

Уторак, 5. мај 2020.

час 123. 

 

 

 

понедељак, 4. мај 2020.

час 122.

 

 

 

 

 

 

 

 

 

среда, 29. април 2020.

час 121.

 

Данас је био час провере. Стигли су сви задаци, биће прегледани и добићете обавештење о оцени и о самом задатку.

Поред тога, добићете и још по једну формативну оцену, тј. оцену о вашој активности у протеклом периоду.

 

Данашња тема је 

ДУЖИНА КРУЖНОГ ЛУКА

 

Подсетимо се: Кружни лук је део кружнице, ограничен са две тачке.

 

 

 

 До обрасца за израчунавање кружног лука лако можемо доћи на следећи начин:

Поделимо круг на 360 једнаких делова:

Ја, наравно, нисам могао да поделим овај круг баш на 360 делова, али и ова подела је довољна да се уочи суштина. Дакле, обележени део представља један од 360 једнаких кружних лукова. Како их има 360, и сви су једнаки, а знајући да је цела кружница дужине 2𝞹r, онда је лако закључити да је дужина тог лука (где је угао 1 степен) једнака 

Из овога даље можемо да закључимо да би за угао од два степена било 2 пута више, од 3 степена 3 пута више, од 𝛼 степени 𝛼 пута више па је образац:

 

 

Када скратимо 2 и 360, добијемо коначни облик обрасца:

 Дужина кружног луку једнаке је проиводу броја пи, полупречника и централног угла, подељеном са 180 степени.

 Домаћи задатак: израчунати дужину кружног лука круга полупречника 15 цм, чији је централни угао 45 степени.

 

 

 

 

 

 

 

уторак, 28. април 2020.

час 120

 

 

Данас је рађена провера на даљину, у виду писменог задатка, у петом разреду Било је неких техничких потешкоћа, али су петаци имали довољно времена и  да  комуницирају са мном, и са разредном а и да ураде све што треба, тако да све то могу да очекујем и од вас. Имате упутство на задатку: сваки задатак морате преписати јер су код свих различити. Не морате их радити редом: препишете задатак - урадите, препишете други - урадите....

Радите хемијском оловком јер обична се често не види добро са фотографије. Сликајте УСПРАВНО, да не морам ја да окрећем те слике. Дакле, сутра у 12 сати.

данашња лекција је 

ОБИМ КРУГА

утврђивање

подсећамо се:

 

КОЛИЧНИК ОБИМА КРУГА И ЊЕГОВОГ ПРЕЧНИКА УВЕК ЈЕДАН ИСТИ БРОЈ!!!!

Тај број је назван "Пи"

 

БРОЈ П ЈЕ ИРАЦИОНАЛАН БРОЈ. НАЛАЗИ СЕ НА БРОЈЕВНОЈ ПРАВОЈ ИЗМЕЂУ 3,1415 И 3,1416. ЧЕСТО СЕ УЗИМА ДА ЈЕ ПРИБЛИЖНА ВРЕДНОСТ (ДАКЛЕ НЕ ТАЧНА!!) 3,14

 

 OБИМ СЕ ИЗРАЧУНАВА ПРЕМА ОБРАСЦУ

O = 2rП

 

 

ДОМАЋИ ЗАДАТАК : припремите се најозбиљније за проверу

Многоугао, Правилни многоуглови - конструкције, Зависне величине и њихово графичко представљање, Пропорционалност и пропорције.

 

 

 

 

 

 

 

 

 

 

Понедељак, 27. април 2020.

час 119.

 

 

ОБИМ КРУГА

обрада

 

 

 Откако је Геометрија почела да се развија као једна од  основних математичких  дисциплина, круг је фасцинирао и мислиоце и филозофе и математичаре... И то не без разлога: многи су се трудили да што више сазнају о његовој изузетности и савршености; јер, ако постоји "најидеалнија" геометријска фигура, то је, свакако, круг.

Хиљадама година су математичари премеравали и упоређивали елементе кругова свих димензија, при чему су утврдили да је

КОЛИЧНИК ОБИМА КРУГА И ЊЕГОВОГ ПРЕЧНИКА УВЕК ЈЕДАН ИСТИ БРОЈ!!!!

Тај број је назван "Пи"

 

 Зове се још и ЛУДОЛФОВ БРОЈ.

 

 

  

ДАКЛЕ, КОЛИЧНИК ОБИМА И ПРЕЧНИКА КРУГА

 

 БРОЈ П ЈЕ ИРАЦИОНАЛАН БРОЈ. НАЛАЗИ СЕ НА БРОЈЕВНОЈ ПРАВОЈ ИЗМЕЂУ 3,1415 И 3,1416. ЧЕСТО СЕ УЗИМА ДА ЈЕ ПРИБЛИЖНА ВРЕДНОСТ (ДАКЛЕ НЕ ТАЧНА!!) :

 

Обзиром да је пречник једнак збиру два полупречника имамо да је

 тако да коначно добијамо образац за израчунавање ОБИМА КРУГА:

 

O = 2rП

 

 Пример: Израчунати обим круга чији је полупречник 10cm.

O = 2rП

О = 2∙ 10 ∙П

O = 20П

 

ДОМАЋИ ЗАДАТАК : припремите се најозбиљније за проверу која ће бити у среду:

Многоугао, Правилни многоуглови - конструкције, Зависне величине и њихово графичко представљање, Пропорционалност и пропорције.

 

 

 

 

 

 

 

Четвртак 23.април 2020.

час 118.

 

Добио сам неколико мејлова са домаћим задацима, али ни једно обавештење да сте прочитали и разумели обавештење о писменом задатку. Зато га постављам поново:

у среду 29. априла, радићете писмени задатак. Тога дана ће свако од вас у 12 сати добити задатке које треба да уради, фотографише, и те  фотографије пошаље на мој мејл најкасније до 13 сати и петнаест минута. Задатке ћете добити на мејл адресе са којих сте ми се до сада јављали. Задаци ће бити из области које смо радили у периоду од другог писменог: Многоугао, Правилни многоуглови - конструкције, Зависне величине и њихово графичко представљање, Пропорционалност и пропорције. Свако од вас ће имати задатке исте тежине али са другачијим подацима.

Напомињем да задатке који пристигну после задатог рока нећу узимати у обзир. Молим да овај писмени задатак схватите најозбиљније, јер ћу вам на основу њега дати једну од оцена. АКО ВАМ ЈЕ БИЛО ШТА НЕЈАСНО у вези овог обавештења ПИТАЈТЕ НА ВРЕМЕ!! ТАКОЂЕ, ДА МИ СЕ СВИ ЈАВИТЕ ДОПЕТКА, ДА СТЕ ПРОЧИТАЛИ И РАЗУМЕЛИ ОБАВЕШТЕЊЕ!!

 

 

Данашња наставна јединица је 

ЦЕНТРАЛНИ И ПЕРИФЕРИЈСКИ УГАО КРУГА

 утврђивање

 Поново прочитајте претходни блог!

 Урадићемо два примера израчунавања непознатих углова која су везана за централни и периферијски угао:

 

 

задатак 3 из уџбеника на 138. страни:

На основу података на сликама израчунај колики је осенчени угао:

 

 Видимо да је угао од 82⁰ централни угао, пошто му је теме у центру О. осенчени угао је периферијски над истим луком: знамо да је периферијски угао два пута мањи од централног, значи тражени угао је 41⁰.

 

На слици изнад је непознат централни угао. Угао од 110⁰ је његов периферијски, значи централни је два пута већи и износи 220⁰.

 

 

Ваш домаћи задатак. Уџбеник, страна 138 1 и 2. задатак.

Додатни задатак: иста страна задатак 3, трећа и четврта слика

 

 

 

среда 22.април 2020
час 117.

 ВАЖНО!!ВАЖНО!!ВАЖНО!!

ВАЖНО!!ВАЖНО!!

Драги седмаци, у среду 29. априла, радићете писмени задатак. Тога дана ће свако од вас у 12 сати добити задатке које треба да уради, фотографише, и те  фотографије пошаље на мој мејл најкасније до 13 сати и петнаест минута. Задатке ћете добити на мејл адресе са којих сте ми се до сада јављали. Задаци ће бити из области које смо радили у периоду од другог писменог: Многоугао, Правилни многоуглови - конструкције, Зависне величине и њихово графичко представљање, Пропорционалност и пропорције. Свако од вас ће имати задатке исте тежине али са другачијим подацима.

Напомињем да задатке који пристигну после задатог рока нећу узимати у обзир. Молим да овај писмени задатак схватите најозбиљније, јер ћу вам на основу њега дати једну од оцена. АКО ВАМ ЈЕ БИЛО ШТА НЕЈАСНО у вези овог обавештења ПИТАЈТЕ НА ВРЕМЕ!! ТАКОЂЕ, ДА МИ СЕ СВИ ЈАВИТЕ ДО ПЕТКА, ДА СТЕ ПРОЧИТАЛИ И РАЗУМЕЛИ ОБАВЕШТЕЊЕ!!

 

Данашња наставна јединица је 

ЦЕНТРАЛНИ И ПЕРИФЕРИЈСКИ УГАО КРУГА

 

 

На слици изнад је представљен централни угао круга. То је угао који заклапају два полупречника, а теме угла је у центру круга.

Два полупречника деле круг на два централна угла од којих је један конвексан а други неконвексан (слика испод)

 

 

 За оба угла важе исте особине.

конвексни и неконвексни централни угао

 

 Сваки централни угао има одговарајуће ПЕРИФЕРИЈСКЕ  УГЛОВЕ.  

ПЕРИФЕРИЈСКИ УГАО ЈЕ УГАО ЧИЈИ СЕ ЦЕНТАР НАЛАЗИ НА КРУЖНИЦИ.

 

 

 НАД СВАКИМ ЦЕНТРАЛНИМ УГЛОМ СЕ МОЖЕ НАЦРТАТИ БЕСКОНАЧНО МНОГО ПЕРИФЕРИЈСКИХ УГЛОВА И СВИ СУ МЕЂУСОБНО ПОДУДАРНИ!!(слика испод)

 

 

ВАШ ДОМАЋИ: одговорити на контролна питања која се налазе на страни 137 у уџбенику.

 

 

 

 

 

уторак 21.април 2020

час 116

КРУГ

понављање

 

КРУГ ЈЕ ДЕО РАВНИ, ОГРАНИЧЕН КРУЖНИЦОМ. Кружница је затворена крива линија код које је свака тачка подједнако удаљена од центра круга.

 

на слици изнад виде се основни елементи круга:

1. кружница

2. полупречник

3. пречник

4. центар круга

као и две праве, тангента и сечица, кружни лук и тетива и централни угао.

 

 

Потсетимо се:

 

кружница је затворена крива линија код које је свака тачка на једнаком растојању од центра круга.

Полупречник је растојање од центра круга до било које тачке на кружници.

Пречник је највеће могуће растојање између две тачке на кружници. Његова дужина је једнака збиру два полупречника.

Центар круга је тачка која је подједнако удаљена од сваке тачке на кружници.

Тангента је права која сече кружницу (додирује је) у једној тачки. Увек је под правим углом у односу на одговарајући полупречник.

Сечица сече кружницу у две тачке. На тај начин прави кружни одсечак.

Кружни лук је део кружнице ограничен са две тачке.

Тетива је дуж која спаја две крајње тачке кружног лука.

Централни угао је угао између два полупречника. Његово теме је центар круга.

 

ДОМАЋИ задатак: НАЦРТАТИ КРУГ, УНЕТИ СВЕ НАВЕДЕНЕ ЕЛЕМЕНТЕ И НАПИСАТИ ДЕФИНИЦИЈЕ.

 

  

 

 

среда, 15.април 2020.

час 114-115

 

 

 

ЗАВИСНЕ ВЕЛИЧИНЕ

систематизација

 

 Зависне су оне величине код којих промена једне изазива промену друге величине.

Зависност може бити ДИРЕКТНА и ОБРНУТА. 

Код директне зависности раст (или опадање) вредности једне величине изазива раст (или опадање) друге,

Код обрнуте зависности раст једне величине изазива опадање друге и обрнуто.

Однос између две величине назива се РАЗМЕРА.

Једнакост две размере назива се ПРОПОРЦИЈА. Општи облик је

 a : b = c : d

 

Пропорција је алгебарски израз у коме су присутне четири величине, од којих су три познате а четврта треба да се израчуна.

Решавање пропорције се ради по систему СПОЉАШЊИ ПУТА СПОЉАШЊИ = УНУТРАШЊИ ПУТА УНУТРАШЊИ.

Примена пропорција је веома раширена у разним научним областима и дисциплинама: математици, хемији, географији, геометрији, физици...

Приликом постављања пропорције најважније је утврдити ВРСТУ ЗАВИСНОСТИ, а до закључка се долази посматрањем промена, тј. да ли су ДИРЕКТНЕ ИЛИ ОБРНУТЕ.

Приликом постављања пропорције КАО ПОМОЋ КОРИСТИМО стрелице, а њихова орјентација нам показује како да поставимо пропорцију.

Домаћи задатак:

Уџбеник, страна 131, задаци 9 и 12

Додатни задатак:

Уџбеник, страна 131, задатак 11

 

 

 

 

 

 

 

 

 

 

 

 

 

уторак, 14.април 2020.

час 113

 

 

Драги седмаци, после првих двадесетак дана добили сте и прве оцене активности. Већина вас је била и остала  врло активна, и сходно томе и добро оцењена. Разумљиво је да нисмо могли сви одмах и у истој мери да се пребацимо на овакав начин наставе, из много разлога који су мање или више оправдани. Ускоро ће бити почето и са бројчаним оцењивањем пошто смо неке области завршили. Ваше је да пратите ТВ учионицу, и наставу коју држим преко овог блога, и да се потрудите најбоље што можете у овом тренутку. По задацима које добијам видим да напредујете, и то је за сваку похвалу. Ипак, неки од вас ВРЛО НЕРЕДОВНО ШАЉУ ЗАДАТКЕ, јер очигледно да неки родитељи и ученици не схватају у довољној мери озбиљност ситуације у којој се налазимо и начина на који покушавамо да превазиђемо ту ситуацију.

 

 

Данашња наставна јединица је 

ПРИМЕНА ПРОПОРЦИЈА

 

Прегледам задатке који стижу, неки од вас раде задатке свакодневно, на чему не инсистирам, али што је за сваку похвалу. Међутим, имам и неке замерке: журите (не сви) и не посветите се довољно задатку. Пропорцију је лако решити (мада сам приметио код мањег броја ученика да не множе по правилу СПОЉАШЊИ СА СПОЉАШЊИМ)а најтежи део задатка је закључити каква је врста зависности. На пример, у задатку коме сам тражио да утврдите врсту зависности времена за које тркач стигне и његовог освојеног места, готово сви сте одговорили да је директна зависност. Па како то? Ако је више времена трчао значи да је спорије трчао, а медаље ваљда освајају најбржи? Има још таквих грешака и на њих вас и упозоравам.

 

задатак: За осветљење учионице потребно је укључити 24 сијалице од 75W. колико треба сијалица од 100W.

која је ово зависност?

Ако су сијалице јаче да ли их треба више или мање? 

То вам је домаћи!!

Додатни задатак: Два комплементна угла су у размери 2:7. Које су величине тих углова?

 

 

 

 

 Понедељак, 13,април 2020.

112 час

 

 

 

Данас је на ТВ учионици примена пропорција, дакле вежбање задатака. За прве две недеље сам оценио вашу активност. Већина вас се редовно јављала са задацима, углавном тачним, али има и оних који су се јављали врло ретко па и никако. Подсећам вас да је то за сада једини начин да пратим ваш рад и зато немојте све то олако схватати.

И наша данашња тема се зове

ПРИМЕНА ПРОПОРЦИЈА

а у оквиру ње ћу урадити два задатка и вама задати задатке за домаћи

1.задатак: Од 3кг брашна се добије 140 ђеврека. колико брашна треба за 140 ђеврека?

Видимо да је зависност између броја ђеврека и количине брашна ДИРЕКТНА јер за ВИШЕ ЂЕВРЕКА треба ВИШЕ БРАШНА:

 

 Стрелице стављамо у исти смер и пишемо:

х : 3 = 140 : 28 

28 ∙ х = 3 ∙ 140

28х = 420

х = 420 : 28

х = 15

 

2. задатак: Примена пропорције за задатак из физике. 

Ако се воз креће брзином од 80km/h прећи ће предвиђени пут за 2 сата и 30 минута. Којом брзином треба да се креће воз да би стигао на време, ако је у старту закаснио пола сата? 

Размислимо: воз касни, а да би стигао на време да ли треба да пожури? Наравно. А у каквој су зависности време вожње и брзине?

Што је ВЕЋА БРЗИНА кретања, треба му МАЊЕ ВРЕМЕНА: То је ОБРНУТА ЗАВИСНОСТ

 

 пишемо: 

х : 80 = 2,5 : 2

2х = 80 ∙ 2,5

2х = 200

х = 100

Дакле, воз треба да иде 100km/h да би стигао на време.

Домаћи задатак: 

1. Бициклиста пређе 9km за 15 минута. За које време ће прећи 12,6 km ?

2. Зидар заврши неки посао за 12 дана ако ради 10 сати дневно. Колико му дана треба ако ради 8 сати дневно?

ДОДАТНИ ЗАДАТАК:

Два радника треба да поделе зараду од 19800 динара. Како да поделе ако је један радио 4 а други 5 дана?

 

 

 

 

 

 

 

 

 

 

четвртак 9.април 2020.

час 111

 

ПРИМЕНА ПРОПОРЦИЈА 

 

Пропорције су веома користан "рачунски алат", са којим се лако ради. Зато имају велику примену у самој математици, али велику примену и у хемији, физици, географији, статистици итд... И што је такође важно - у свакодневном животу. Ако се само мало потрудите, нећете имати никаквих проблема у израчунавањима процентних раствора у хемији, израчунавању растојања са географске карте и слично.

Из оних радова које сте послали видим да сте научили принцип самог решавања пропорције. Оно што нам преостаје да вежбамо је КАКО ДА ПРЕПОЗНАМО величине које треба да убацимо у пропорцију, и како да препознамо која врста зависности је у питању.

А то ћемо постићи вежбањем и решавањем задатака.

1. Задатак из географије:

 Карта је рађена у размери 1 : 200 000. Ако је растојање између два места на карт 3,7 цм, колико је то растојање у природи?

Приметио сам да су вам ови НАЈПРОСТИЈИ задаци тешко схватњиви. Али познавање пропорција ће нам помоћи.

Које су величине присутне? величина на карти и величина у природи.  А у каквој су зависности? да ли повећање величине у природи значи и повећање на карти? Да!! Значи, директна зависност.

величина на карти                                величина у природи

1                                                    200 000

↑         3,7                                                         х                ↑   

па је пропорција

х : 200 000 = 3,7 : 1

х ∙ 1 = 200 000 ∙ 3,7

х = 740 000 cm

када центиметре претворимо у километре ( 1 km има 100 000 центиметара ) то је 7,4 km

 

2. задатак из геометрије:

Страница квадрата је 4 cm. Израчунај обим квадрата чија је страница три пута већ од странице датог квадрата.

  

знамо да квадрат има четири једнаке странице. Ако је једна страница 4 cm, онда ће обим бити 4 ∙ 4 = 16 cm. Зависност је директна, јер што је већа страница већи је и обим.

 

 величина странице                             обим

4                                                             16

↑        3 ∙ 4 = 12                                                             х       ↑              

х : 16 = 12 : 4

4х = 16 ∙ 12

4х = 192

х = 192 : 4

х = 48cm

 

 Толико за данас. Домаћи : Збирка, 57 стр, задатак 17

Додатни задатак: стр 57 зад 16 и 18  ( није обавезно, али је препоручљиво)

 

 

 

 

 

 

 

 

среда, 8.април 2020. 

час 110

Драги седмаци, настављамо са пропорцијама. Назив данашшње лекције је исти као и јучерашње на РТС-у

СВОЈСТВА ПРОПОРЦИЈА

 

ПОДСЕТИМО СЕ:

Пропорција је израз у коме имамо четири величине. Служи нам да израчунамо једну кад имамо три познате.

Пропорцију решавамо тако што  множимо спољашњи број са спољашњим и унутрашњи са унутрашњим. Тако добијамо једначину коју лако решимо.

Главно је утврдити врсту зависности, затим обележимо стрелицама и добијемо пропорцију.

данас ћу решити задатак код кога је у питању обрнута пропорционалност:

Задатак:  три радника копају шанац дужине 100 метара. за тај посао им је потребно 10 дана. Колико дана би трајао посао ако би радило 5 радника?

Решење:   Које су овде величине које су повезане? То су БРОЈ РАДНИКА И БРОЈ ДАНА. Дужина шанца је овде неважна, она је и дата да вас збуни. РАЗМИШЉАМО О ВРСТИ ЗАВИСНОСТИ: да ли ће више радника радити више или мање дана? МАЊЕ! Дакле, обнута зависност. Задатак постављамо као на слици испод:

 

 

И сада је пропорција:

х : 10  =  3 : 5

одакле је  

х ∙ 5 = 3 ∙ 10

па је 

5х = 30

и

х = 30 : 5 = 6 дана

 

 

Домаћи задатак: Збирка, страна 53, задатак 2.

Додатни задатак: страна 53, задатак 3

уторак, 7.април 2020.

час 109

 

 

Драги седмаци, од данас ћу, осим обавезног задатка за домаћи, давати и предлог задатка вишег нивоа. Тај задатак нисте у обавези да урадите, он је изазов за оне ученике који желе да постигну боље резултате.

 

 Данашња наставна јединица је 

               РАЗМЕРА И ПРОПОРЦИЈА

 

Шта је то размера?

Размера је количник два броја!

Нпр:      број 3 и број 2 стоје у размери ТРИ ПРЕМА ДВА, а то се пише 3 : 2 

У којој размери стоје бројеви 2 и 11?

У размери 2 : 11

А 3,2 и 1, 5=?

У размери 3,2  : 1,5

Као и код разломака, погледамо да ли можемо скратити израз! Рецимо бројеви 5 и 10 стоје у размери  5 : 10. Оба броја су дељива са 5, тако да размеру 5 : 10 можемо да напишемо као 1 : 2.

 

 А шта је пропорција?

ПРОПОРЦИЈА ЈЕ ЈЕДНАКОСТ ДВЕ РАЗМЕРЕ. 

На пример

 5 : 10 = 1 : 2

у општем облику

a : b = c : d

 

Kако то рећи просто? Пропорција је израз у коме имамо четири величине. Служи нам да израчунамо једну кад имамо три познате.

Пример: 

2 : 5 = 3 : х 

Како израчунати непознату величину? 

Поступак је следећи: множимо спољашњи број са спољашњим и унутрашњи са унутрашњим, као на слици доле

и добијамо

2х = 15

одатле је

х = 15 : 2 = 7,5 

Како то применити?

 На пример:

3 кг  јабука кошта 360 динара. Колико кошта 4,5 кг? 

ВЕОМА ВАЖНО!!

Знамо да имамо директну зависност и обрнуту зависност. Морамо УТВРДИТИ ВРСТУ ЗАВИСНОСТИ да би поставили пропорцију. Како то радимо? Па ево за овај задатак погледамо величине: прва је количина јабука а друга њихова цена. Ако расте количина јабука расте и њихова цена, зар не? Дакле, у питању је директна зависност!!

То записујемо на следећи начин:

Видите да количина јабука има две вредности које пишемо једну испод друге, а цена такође две, које пишемо једну испод друге. Утврдили смо да је ДИРЕКТНА ЗАВИСНОСТ па стављамо стрелице, као на следећој слици:

Те стрелице су у истом смеру јер је зависност директна. Код обрнуте зависности смер стрелица је супротан (пример касније!!)

Те стрелице нам помажу да напишемо пропорцију. Увек када постављамо стрелице гледамо где се налази непозната и ту стављамо почетак стрелице. 

и сада пишемо:

х : 360  = 4,5 : 3

рачунамо спољашњи пута спољашњи једнако унутрашњи према унутрашњем

3х = 360 ∙ 4,5

3х = 1620

х = 1620 : 3

х = 540

Домаћи: збирка, 58 стр зад 19

Задатак вишег нивоа: збирка, 53 стр зад 19

 

 

 

 

 

 

 

Понедељак 6.април.2020.

Час 107 и 108.

ОБРНУТА ПРОПОРЦИОНАЛНОСТ

Из наслова видите да поред дирекне пропорционалности постоји и обрнута пропорционалност. Код директно пропорционалних величина ( у питању су две величине) однос је следећи: колико пута се повећа једна величина за толико се повећа и друга. На пример, слика троугла: ако троугао повећамо два пута, свака његова страница ће се повећати два пута.

 

 

 Ако се, на пример, потрошња струје смањи за ти пута, онда ће се и рачун за струју смањити три пута, јер су потрошња струје и рачун за струју директно пропорционалне величине.

А шта би биле обрнуто пропорционалне величине?

Погледајмо пример:  Молер кречи собу. За једну собу му треба један дан. Ако би била два молера (који раде истом брзином), колико би им времена требало за исту собу?

Ако једном треба један дан, двојици ће требати дупло мање, тј. пола дана. Тројици би требало трећина дана, четворици четвртина, итд. Дакле, што је њих ВИШЕ, посао ће трајати МАЊЕ. Можемо да кажемо да количина посла и број радника стоје у обрнутој пропорционалности.

Значи, када имамо две величине, које се понашају тако, да ако се једна промени на неки начин и друга се мења, али на супротан начин онда су оне у обрнутој пропорционалности.

Да закључимо:  код ДИРЕКТНЕ  пропорционалности, (ако су наше величине х и у) 

кад х расте и у расте.

кад се х смањује и у се смањује.

 кад х убрзава и у убрзава.

кад х пада и у пада.

Код ОБРНУТЕ пропорционалности, све је обрнуто!!

кад х расте  у се смањује.

кад се х смањује и у се повећава.

 кад х убрзава  у успорава.

кад х пада  у скаче.

 

Размислите и за домаћи напишите који од следећих примера припада директној а који обрнутој пропорционалности:

1. Време трчања такмичара и освојено место. Која је ту зависност?

2. Пређени пут и дужина вожње. Која је ту зависност?

3. Број радника који фарбају и величина офарбане површине. 

Која је ту зависност?

4. Број радника и време фарбања.  Која је ту зависност?

5. Величина троугла и његов обим.  Која је ту зависност?

 6. Величина собе коју треба окречити и број молера?

Која је ту зависност?

 

 

 

 

 

 

 

 

 

Петак, 3.април 2020.

   час 105 и 106.

 

ДИРЕКТНО ПРОПОРЦИОНАЛНЕ ВЕЛИЧИНЕ 

Најпростије ствари је често веома тешко објаснити. Из мог искуства, пропорционалност, пропорције, размера, су управо појмови које ђаци тешко схватају и усвајају, иако су њима свакодневно окружени и свакодневно их користе.

Наша реч за пропорционалност је СРАЗМЕРНОСТ. 

Да би се уопште говорило о пропорционалности потребне су најмање две величине. 

 Погледајте слику:

Видите да је на све три слике исти лик. Пардон, ПОТПУНО ИСТИ ЛИК. Али има разлике. У чему ? У величини!!! Слика 2 је два пута мања од слике 1 а слика 3 је два пута бећа од слике 2. То је зато што су слике 2 и 3 ПРОПОРЦИОНАЛНО СМАЊЕНЕ ОДНОСНО УВЕЋАНЕ  у односу на слику 1. Дакле, сваки елеменат, апсолутно сваки, са слике 1 је или два пута умањен (слика2) или два пута увећан. Сваки елеменат је ПРОПОРЦИОНАЛНО УВЕЋАН (УМАЊЕН).

 

Примера ради, ево друге слике:

 

 Видите да слика 2, иако личи, НИЈЕ ИСТА као слика 1. То је због НЕПРОПОРЦИОНАЛНОГ (НЕСРАЗМЕРНОГ) увећања.

 У математици, а и у другим наукама, пропорционалне величине су оне чији је однос константан. Преведено на наш језик, кад се једна подели са другом увек добијамо исти број.

ПРИМЕР: Једна чоколада кошта 100 динара. Ту имамо две величине: чоколаду и цену чоколаде. Када једну величину поделимо са другом (то значи "однос две величине") добијемо

100 : 1 = 100

Две чоколаде коштају 2 х 100, тј 200 динара. Однос је

200 : 2 = 100

За три чоколаде је 

300 : 3 = 100

Лако је видети да је однос између чоколаде и нјене цене 100, и тај број називамо КОЕФИЦИЈЕНТ ПРОПОРЦИОНАЛНОСТИ.

Домаћи задатак:

Знате да је за једну чашу сока потребно 2 кашичице Цедевите.

Треба вам сок за три другара и вас. 

1. Колико треба кашичица за вас четворо? 

2. Који је ту коефицијент пропорционалности?

3. Ако ставите 20 кашичица, колико је то чаша сока?

Уторак 01.04.2020.

час 104.

 

 

 

 

 

 

 

 

 

четвртак, 26.март 2020.

час 101.  

 

Драги седмаци, прескочили смо термин који нам је био резервисан за трећи писмени задатак. Због ове ситуације нисмо у могућности да то урадимо, али је сигурно да ћемо ту проверу морати да извршимо и то у скорије време. На каоји начин ће то бити - сазнаћете ускоро.

Неки од вас су јако вредни, и задатке шаљу свакодневно. Други су нешто спорији, и то им не замерам, али један ученик ми се уопште није јавио, а то није добро. Нико од нас, а то сте сви ви и ја, као ваш наставник, дакле, нико није ослобођен обавеза, и то сви треба да имамо на уму. Данас ћемо причати о ономе што смо јуче започели а то је 

РАСТОЈАЊЕ ИЗМЕЂУ ДВЕ ТАЧКЕ У КООРДИНАТНОЈ РАВНИ

 

На слици испода сам вам приказао како се рачуна растојање између две тачке које су на различитим удаљеностима од координатних оса (јуче сам такође дао пример 5)

 

 

На слици видите да је непознато растојање дуж АВ. Она се рачуна преко ПИТАГОРИНЕ ТЕОРЕМЕ, јер та дуж гради правоугли троугао са дужима АС и СВ. Она је ХИПОТЕНУЗА. Катете очитамо: видимо да је АС = 7 - 3 = 4  а СВ = 6 - 3 = 3

 

 

Ваш домаћи је : израчунати ПОВРШИНУ троугла који праве тачке А(- 2, 2)  В(2, 2) и С(-2, 5) 

 

ПОМОЋ: треба унети дате тачке у координатни систем. Повезивањем добијате троугао. Подсетите како се рачуна површина троугла!!!!! (основица пута...)

 

 

 

 

 

 

среда, 25.март 2020.

100. час

Драги седмаци, ево и стотог часа. А неки од вас ми се још увек нису јавили нити послали домаће задатеке.
Школа је и даље обавезна, иако смо у ванредном стању. Већ сам више пута писао да нећу бити у могућности да вас оценим уколико не сарађујете са мном и не обављате задатке које добијате на овом блогу.

 

Наша данашња наставна јединица је 

РАСТОЈАЊЕ ТАЧКЕ У КООРДИНАТНОЈ РАВНИ

 

Лекција се налази на 116. страни вашег уџбеника.

Свака тачка има ПОТПУНО ОДРЕЂЕН ПОЛОЖАЈ у координатној равни. Зато се и свако растојање између две тачке може израчунати. Да бисмо то урадили, потребно је да разликујемо неколико случајева.

СЛУЧАЈ 1: тачке се налазе на истом растојању од осех и на истој страни у односу на осу у.

 Ако се тачке налазе на истом растојању од осе х, њихово се међусобно растојање рачуна како је приказано на слици испод

 

 

СЛУЧАЈ 2: тачке се налазе на истом растојању од осех и на супротним странама у односу на осу у.

 Ако се тачке налазе на истом растојању од осе х, њихово се међусобно растојање рачуна како је приказано на слици испод

 

 

 СЛУЧАЈ 3 и 4:   тачке се налазе на истом растојању од у осе, а на истој страни осе х (први цртеж на слици доле) или на различитим странама осе џ (други цртеж)

 

 

 Видите да се и ту на исти начин рачуна растојање: на првом цртежу је 6 - 2 = 4   а на другом  4 - ( -6) = 4 + 6 = 10

СЛУЧАЈ 5 је општи случај, када тачке нису на једнаком удаљењу од оса, па чак нису ни са истих страна.  У том случају формирамо правоугли троугао и решавамо Питагорину теорему!!ПОГЛЕДАЈ слику ДОЛЕ!!

 

 

 Видите да страницу ВС и страницу АС очитавамо као у случајевима 1-4, и после рачунамо преко ПИТАГОРИНЕ ТЕОРЕМЕ.

 

 ДОМАЋИ ЗАДАТАК:  уџбеник, страна 117, задаци 1 и 2.

 

 

 

 

 

 

 

 

УТОРАК, 24.МАРТ 2020.

99. ЧАС

 

 Данашња наставна јединица је 

ПРАВОУГЛИ КООРДИНАТНИ СИСТЕМ У РАВНИ

Јучерашњи домаћи задатак је био да напишете ваш закључак о томе како се уписују и читају тачке у равни помоћу координатног система. УВЕК се прво чита (или пише) Х координата,  а као друга У координата!! 

ПРИМЕР:

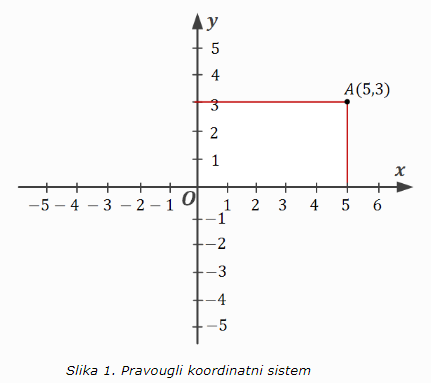
 На слици изнад видимо тачку А. Њене координате су 5 и 3. Та се тачка означава као А(2, 3). Из тачке повучемо ПРВО вертикалу (праву паралелну са у осом). Број у којој она сече х осу је х-координата (у нашем случају 5). Затим се повлачи права паралелна са х осом до пресека са у-осом и очитава број који представља у-координату.

 

ДОМАЋИ ЗАДАТАК: нацртати ТРИ координатна система. У ПРВИ унети тачке А(-1 ,3) и В(1,  -3).  У ДРУГИ унети А(4, 2)  В(4,  -2)   С(-4,  2) и D(-4,  -2).  У ТРЕЋИ унети А(2, 3) и 

В(3, 2)

 

 

 

 

понедељак, 23. март 2020.

час 98.

Драги седмаци, прва недеља је за нама. Још увек је за све нас ова ситуација нова и необична: неки су се брзо снашли, а некима треба више времена . Оно што је сигурно је да ће ова ситуација потрајати и, хтели ми то или не, на њу ћемо морати да се навикнемо. Овај блог је првенствено намењен томе да вам дам смернице и упутства како да користите интернет у настави математике. На њему ћу покушати да спојим часове са телевизије и са Јутјуба, уз неке моје коментаре и објашњења. 

Оно што сам до сада могао да закључим је следеће: нисте довољно озбиљно схватили ситуацију у којој се налазимо о мере које предузимамо да превазиђемо ту ситуацију. Ваша је ОБАВЕЗА да пратите предвиђени програм, ваша је обавеза и да имате комуникацију са наставницима, ваша је обавеза да поштујете и испуњавате захтеве које вам наставници постављају. Што се Математике тиче, за сада је једини начин да вршим проверу вашег напредовања преко мејла који ми шаљете.

Неки од вас се још нису јавили, други шаљу нетачне задатке уз изговор „ја то не умем“. Чињеница је да немамо директну комуникацију, али ја се трудим да дам потребна појашњења. Ипак то није довољно. Позитивна ствар која је проистекла из ове ситуације је то да лекције можете погледати више пута, јер стоје на серверима. Видео можете враћати, прекидати, настављати, све док вам не буде јасно о чему се у њему говори. Програм на РТС3 прати наше лекције, и ја га гледам и тврдим да наставници веома лепо и јасно објашњавају градиво које обрађујемо.

РТС Планета тренутно не прати наше наставне јединице, али како време протиче, све ће се ускладити и биће потребно да поново погледате те наставне јединице. Тренутно је на РТС Планети проучавање полинома, а то је област коју смо ми одрадили. Добро је одгледати те лекције да бисте утврдили то градиво. И ПРЕДАВАЊА ИЗ СВИХ ОСТАЛИХ ПРЕДМЕТА СЕ НАЛАЗЕ ТАМО ТАКО ДА САМ И ВАМА ДАО УПУТСТВО КАКО ДА СЕ ПРИЈАВИТЕ И УЛОГУЈЕТЕ. РТС Планета се  налази на следећем линку:

https://rtsplaneta.rs/video/show/1347472/  

Морате се пријавити и улоговати на сајт, а да бисте то урадили пратите следеће кораке :

КОРАК 1 : када одете на сајт очекује вас следећи прозор

Притиском на дугме ПРИЈАВИТЕ СЕ отвара се следећи прозор

КОРАК 3 : РЕГИСТРУЈТЕ СЕ БЕСПЛАТНО. Притиском на ту опцију добијате следећи прозор:

КОРАК 4: Попуните сва поља, при чему сами бирате лозинку (запишите је негде да бисте је нашли ако је заборавите)

КОРАК 5. Добијате мејл, у коме треба да притиснете црвено думе на коме пише "потврди и ваша мејл адреса.

КОРАК 6: Добијате још један мејл у коме се потврђује ваша регистрација.

Пошто сте се успешно регистровали, идете на адресу

https://rtsplaneta.rs/video/show/1347472/ 

ПОПУНИТЕ ПОЉА ЗА ПРИЈАВЉИВАЊЕ И ТО ЈЕ СВЕ.

Када одете на тај линк видећете слику коју сам поставио  испод

Притиском на "Моја школа" (заокружено црвеном оловком) одлазите на страну

 где бирате "Основна школа" и то вас води на

 где бирате ваш разред.(на слици је изабран осми, ви бирате, наравно, седми) То вас коначно уводи у ваш разред, где имате садржаје свих емисија по предметима, редом којим су емитоване. Кликом на сваки од понуђених прозорчића улазите на емисију. СВАКУ ОД ТИХ ЕМИСИЈА МОЖЕТЕ ГЛЕДАТИ КОЛИКО ГОД ПУТА ЖЕЛИТЕ.

 

Поред ПЛАНЕТЕ РТС ја вам постављам и корисне линкове са Јутјуба, на којима су урађена квалитетна објашњења и примери. Дакле, дато вам је пуно квалитетних могућности, све остало зависи од вас. 

 Наша данашња наставна јединица је

ПРАВОУГЛИ КООРДИНАТНИ СИСТЕМ У РАВНИ

Лекција се налази у  уџбенику, на странама 113 -116 

Правоугли координатни систем у равни

  Систем представљен на горњој слици се састоји од две бројевне праве које се секу под правим углом у тачки 0. Вертикална права се назива ОРДИНАТА и означава словом у. Хоризонтална права се назива АПСЦИСА и обележава се са х. Заједно се називају КООРДИНАТЕ. Често се називају и х-оса и у-оса.

Овај систем служи за тачно позиционирање било које тачке у равни. СВАКА ТАЧКА ИМА ДВЕ КООРДИНАТЕ: Х и У. Координате сваке тачке се задају тако што се ПРВО ПИШЕ ВРЕДНОСТ ЗА Х, А ЗАТИМ ЗА У.

 

 

 

 На слици изнад су римским бројевима означени КВАДРАНТИ који настају пресеком две бројевне праве. Видите на слици ознаке + и - . Знамо да свака бројевна права има позитивне и негативне делове.Тако квадранту 1 припадају позитивни делови обе праве, другом један позитивни и један негативни и тако редом.

Бројевне праве су подељене на ЈЕДИНИЧНЕ ВРЕДНОСТИ. Наносе се бројеви редом, на подједнаком растојању.

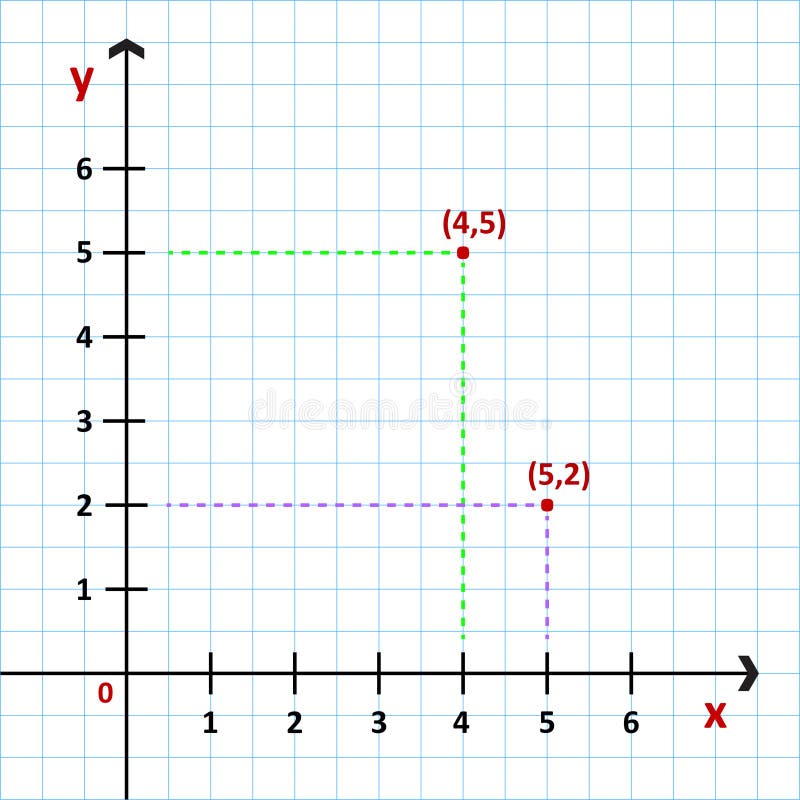
На следећој слици су приказане две тачке којима је одређен положај у равни.

 ВАШ ДОМАЋИ ЗАДАТАК ЈЕ: ПРВО ОБАВЕЗНО ПОГЛЕДАТИ ВИДЕО НА АДРЕСИ

 https://www.youtube.com/watch?v=CeYwQLiLl9o

А ЗАТИМ У СВЕСЦИ НАПИСАТИ НА КОЈИ НАЧИН СУ ДАТЕ ТАЧКЕ ПОЗИЦИОНИРАНЕ У КООРДИНАТНОМ СИСТЕМУ.

 

 

 

 

петак, 20.март 2020.

час 97.

Драги седмаци, ова прва недеља је за нама, неки од нас су се снашли добро, неки мање добро, али је битно да се сви трудимо. И ми, наставници, имамо свакодневне обуке које су за нас новина, па се трудимо да се све то некако уклопи у овај наш заједнички посао. 

Што се тиче домаћих задатака, неки од вас су кренули да их шаљу свакодневно, али неки нису до сада ништа послали. Подсећам вас да је овај петак, рецимо до 9 сати увече, крајњи рок за израду и слање домаћих задатака. Такође вас подсећам да је то ВАША ОБАВЕЗА!! 

Све то је неопходно да бих магао сваки задатак да проверим и сваком од вас послао сугестију или потребно објашњење. По ономе што сам до сада видео, углавном сте то урадили и тачно и педантно. Градиво за седми разред није лако ни у нормалним условима, тако да вас саветујем да свему овоме посветите пуну пажњу и дате вој максимум.

 

наша данашња наставна јединица су и даље многоуглови

 

МНОГОУГЛОВИ 

систематизација градива

 

 

Подсетимо се најважнијих дефиниција: 

Многоугао, који се назива још и полигон је до равни ограничен затвореном изломљеном линијом која не сече саму себе. 

Сваки многоугао има исти број страница, темена и углова.

Име добија према броју углова: троугао, четвороугао, петоугао....

Постоје конвексни и неконвексни многоуглови. 

Троугао је први у низу, са најмањим могућим бројем углова.

Правилни многоуглови имају све странице подударне и све углове подударне.

Дијагонала многоугла је дуж која спаја несуседна темена. Број дијагонала из једног темена се рачуна по обрасцу : d = n - 3

Укупан број дијагонала се рачуна по обрасцу:    D = n(n - 3)/2

Збир углова многоугла се рачуна по обрасцу:   S = (n - 2) 180

Угао правилног многоугла се израчунава тако што се прво израчуна укупан збир, а затим подели бројем углова!!

Обим многоугла је једнак збиру дужина свих страница.

Површина правилних многоуглова се рачуна преко карактеристичних троуглова, Код неправилних помоћу израчунаванња површина мањих фигура које се могу уцртати у дати многоугао.

 Ваш задатак:  

1. Одреди број дијагонала из једног темена, укупан број дијагонала, збир свих углова и величину угла код ПРАВИЛНОГ шестоугла. Израчунати његов ОБИМ и ПОВРШИНУ ако се зна да је дужина његове странице 10 центиметара.

2. Конструиши правилан осмоугао уз помоћ квадрата чија је дијагонала 10 центиметара.

Ове задатке послати најкасније сутра, до 14 часова.

 

 

 

 

четвртак, 19.март 2020.

час 96

Драги седмаци, ево нас на трећем часу. Данас настављамо претходну лекцију, а надам се да сте погледали и лекцију на телевизији, која се односи на полиноме. Са некима од вас је већ почела комуникација, неки се још нису јавили, али ми сви схватамо да је овај начин потпуно нов за све нас, и свако за сваког има довољно и разумевања и стрпљења. Задаци које вам задајем су минимум ваше обавезе. Сви имате и уџбенике и збирке, и било би веома корисно да урадите и по неки задатак који нисам задао. Потрудите се да се у будуће потписујете на крају сваког задатка, то ми је потребно ради касније евиденције. Подсећам да је недељни крајњи рок за домаће ПЕТАК!!

 

Назив данашње наставне јединице је

 

 ОБИМ И ПОВРШИНА МНОГОУГЛОВА  

систематизација градива

 

 

Подсетимо се најважнијих дефиниција: 

Многоугао, који се назива још и полигон је до равни ограничен затвореном изломљеном линијом која не сече саму себе. 

Сваки многоугао има исти број страница, темена и углова.

Име добија према броју углова: троугао, четвороугао, петоугао....

Постоје конвексни и неконвексни многоуглови. 

Троугао је први у низу, са најмањим могућим бројем углова.

Правилни многоуглови имају све странице подударне и све углове подударне.

Дијагонала многоугла је дуж која спаја несуседна темена. Број дијагонала из једног темена се рачуна по обрасцу : d = n - 3

Укупан број дијагонала се рачуна по обрасцу:    D = n(n - 3)/2

Збир углова многоугла се рачуна по обрасцу:   S = (n - 2) 180

Угао правилног многоугла се израчунава тако што се прво израчуна укупан збир, а затим подели бројем углова!!

Обим многоугла је једнак збиру дужина свих страница.

Површина правилних многоуглова се рачуна преко карактеристичних троуглова, Код неправилних помоћу израчунаванња површина мањих фигура које се могу уцртати у дати многоугао.

 

 

 Данашњи линк води до туторијала који показује конструкцију правилног шестоугла и његових дијагонала.

 

 https://www.youtube.com/watch?v=bfinQbbwr6s

 

 

 ДОМАЋИ ЗАДАТАК: Преписати у свеску за домаћи ове дефиниције и конструисати правилни шестоугао.

 

 

 

 среда 18.март 2020.
 час 95.

Драги седмаци, данас је на РТС3 одржан час у вези са сабирањем полинома. Ако сте одгледали тај час (а добро знате да вам је то обавеза), то је онда била добра прилика да се потсетите те лекције коју смо радили и обрадили, а надам се и усвојили у наше знање. Ми нећемо наставити даље о полиномима, јер тада не бисмо имали довољно термина да завршимо оно што смо започели. Зато је наша данашња тема 

ОБИМ И ПОВРШИНА МНОГОУГЛОВА 

Знамо да је ОБИМ сваког многоугла једнак ЗБИРу дужина СВИХ СТРАНИЦА.

Обим правилних многоуглова је лако израчунати : довољна је дужина само једне странице! Њену величину помножимо са бројем страница и добијемо обим!!

За ову лекцију препоручујем видео који се налази на следећој страници:

Адресу копирате и убаците у претраживач.

http://www.rajak.rs/sr/video-lekcije/sedmi-razred-osnovne-skole/obim-i-povrsina-pravilnog-mnogougla-488.html

Видео, осим дефиниција садржи и неколико урађених и објашњених задатака, везаних за обим и површину правилних многоуглова.

 На слици изнад је приказан правилан шестоугао, поред су написане формуле за обим и површину. Површина правилних многоуглова се своди на израчунавање површина КАРАКТЕРИСТИЧНИХ ТРОУГЛОВА, који се добијају повлачењем највећих дијагонала.

 Површина неправилних многоуглова, као и обим, своди се на уцртавање елемената који могу помоћи у упрошћавању слике (дијагонале, висине и сл...) Као добар пример послужиће вам пример 2 на 110. страни уџбеника.

Ваш домаћи задатак је да тај пример препишете и објасните у свесци за домаћи. ОБАВЕЗНО СЕ ПОТПИСАТИ НА КРАЈУ ЗАДАТКА И НАПРАВИТИ ФОТОГРАФИЈУ ТАКО ДА СЕ НА ЊОЈ ВИДИ И ВАШ ПОТПИС.









уторак, 17.март 2020.
час 94

Драги седмаци, ово нам је први час учења на даљину, и прикључујемо се плану и програму који је актуелан на РТС3. Прилагођавамо се лекцијама које се емитују, тако да ћемо започету тему завршити касније. Лекција која је у току је раније обрађена, тако да ће нам добро доћи да се подсетимо најважнијих делова.

Свакога дана имамо могућност и обавезу да на ТВ РТС3 гледамо и учимо лекције које прате наш план и програм. На овој страни ћете свакодневно добијати задатке и објашњења у вези са лекцијом коју сте одгледали. Сваки разред има посебну страницу, којој приступате притиском на језичак који носи име вашег разреда.

ВАША ЈЕ ОБАВЕЗА да радите домаће задатке и да их НАЈКАСНИЈЕ СВАКОГ ПЕТКА шаљете на мејл адресу коју сам отворио за ту сврху. Можете их слати и свакодневно.

Урађен задатак фотографишете и затим фотографију ПРЕКО ВИБЕРА ПОШАЉЕТЕ НА МЕЈЛ.

Мејл је приказан на насловној страни овог блога, а ево га још једном;

 zoranmakis62@gmail.com

ПОЛИНОМИ, САБИРАЊЕ ПОЛИНОМА 

Полиноми су састављени од елемената који граде полином.  Tи елементи се називају мономи. Сваки моном састоји се од бројевног и словног дела. Словни део чине променљиве а бројевни константе. Te константе се зову коефицијенти.

ПРИМЕРИ МОНОМА:                  - 3а,   xy,     3,      2c 

Мономи који имају једнак словни део, а разликују се само у коефицијенту називају се слични мономи.

САМО СЛИЧНИ МОНОМИ МОГУ ДА СЕ САБИРАЈУ И ОДУЗИМАЈУ!!

ПОЛИНОМИ су рационални бројевни изрази састављени од два или више монома који су повезани операцијама сабирања или одузимања. ПОЛИНОМИ су изрази у којима се НЕПОЗНАТА НЕ МОЖЕ НАЛАЗИТИ НА МЕСТУ ДЕЛИОЦА!!!

 ПРИМЕРИ ПОЛИНОМА:              2x    - 3а,              xy + 2x - 3,  

                                                                    бином                                                    трином

Полиноми се обележавају великим словима латинице.

Домаћи задатак урадити из Збирке, мстрана 28, задаци 1,2,3,4,и5

Толико за први час. Будите вредни, а пре свега - здрави!!